Prüfen Sie ob der Punkt X auf der Geraden liegt.

Question

Aufgabe:

Text erkannt:

2 Prüfen Sie, ob der Punkt $X$ auf der Geraden $g$ liegt.
a) $X(1 \mid 1) ; g: \vec{x}=\left(\begin{array}{l}7 \\ 3\end{array}\right)+t \cdot\left(\begin{array}{r}-2 \\ 3\end{array}\right)$
b) $X(-1 \mid 0) ; g: \vec{x}=\left(\begin{array}{r}-1 \\ 5\end{array}\right)+t \cdot\left(\begin{array}{l}0 \\ 5\end{array}\right)$

Ich wusste leider nicht, wie ich die Vektoren mit der Tastatur schreiben soll, deshalb habe ich die Aufgabe abfotografiert. Ich soll ab und b machen.

Wichtig: ich soll es rechnerisch UND zeichnerisch bestimmen.

Problem/Ansatz:

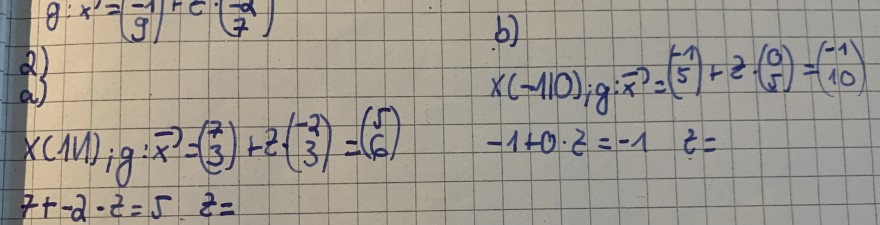
Text erkannt:

2)
$\begin{array}{l} x(111) ; g: \vec{x}=\left(\begin{array}{l} 7 \\ 3 \end{array}\right)+z \cdot\left(\begin{array}{c} -2 \\ 3 \end{array}\right)=\left(\begin{array}{l} 5 \\ 6 \end{array}\right) \\ 7+-2 \cdot z=5 \quad z= \end{array}$
$\begin{array}{l} \text { b) } \\ x(-110) ; g: \vec{x}=\left(\begin{array}{l} -1 \\ 5 \end{array}\right)+z \cdot\left(\begin{array}{l} 0 \\ 5 \end{array}\right)=\left(\begin{array}{l} -1 \\ 10 \end{array}\right) \\ -1+0 \cdot z=-1 \quad z= \end{array}$

Das ist mein Ansatz dazu. Ich habe es mit der Punktprobe gemacht. Ich scheitere jetzt an der Stelle t bei a und b zu bestimmen. Kann mir da jemand helfen? Danach weiß ich, dass ich das in die 2 Zeile der Vektorgleichung einsetzen muss.

Zudem weiß ich leider bei beiden nicht, wie ich das zeichnerisch darstellen soll und würde mich deshalb sehr über Hilfe freuen.

Answer 1

Ortsvektor des Punktes für $\vec x$ einsetzen. Gleichung lösen.

Der Punkt liegt genau dann auf der Geraden, wenn die Gleichung eine Lösung hat.

Comments

Wie komme ich den jeweils auf t als reelle Zahl?

---

Mit Äquivalenzumformungen

---

Was bedeutet denn das? Könnten Sie mir vielleicht erklären, wie ich das mache?

---

$\begin{aligned} \begin{pmatrix}1\\ 1 \end{pmatrix} & =\begin{pmatrix}7\\ 3 \end{pmatrix}+z\cdot\begin{pmatrix}-2\\ 3 \end{pmatrix} & & \left|-\begin{pmatrix}7\\ 3 \end{pmatrix}\right.\\ \begin{pmatrix}-6\\ -2 \end{pmatrix} & =z\cdot\begin{pmatrix}-2\\ 3 \end{pmatrix} & & \left|\cdot\left(-\frac{1}{2}\right)\right.\\ \begin{pmatrix}3\\ 1 \end{pmatrix} & =z\cdot\begin{pmatrix}1\\ \frac{3}{2} \end{pmatrix} \end{aligned}$

Laut erster Komponente muss $z = 3$ sein.

Einsetzen ergibt

        $\begin{pmatrix}3\\ 1 \end{pmatrix}=\begin{pmatrix}3\\ \frac{9}{2} \end{pmatrix}$

Diese Gleichung ist ungültig. Also hat die Gleichung keine Lösung. Deshalb liegt der Punkt nicht auf der Geraden.

---

Alles klar, vielen Dank für die Erklärung.