Definitionsbereich der gebrochen rationalen Funktion: f(x) = 6/(1+e-x)

Question

Ich habe folgende Funktion

$$ f(x) = \frac { 6 }{ 1+{ e }^{ -x } } $$

Dazu soll ich erstmal den Definitionsbereich angeben. Diesen errechne ich doch nur mit den unteren Werten der Funktion, oder?

Kann mir jemand helfen wie ich das berechnen kann? hat das irgendetwas mit einer Verkettungsregel zu tun?

Answer 1

Zur Bestimmung des Definitionsbereiches setzt du den Nenner gleich Null

1+ e^-x = 0

 e^-x = -1

Die E-Funktion ist nie negativ in R daher ist der Definitionsbereich ganz R.

Für die Kurvendiskussion mache ich dir noch zwei Ableitungen

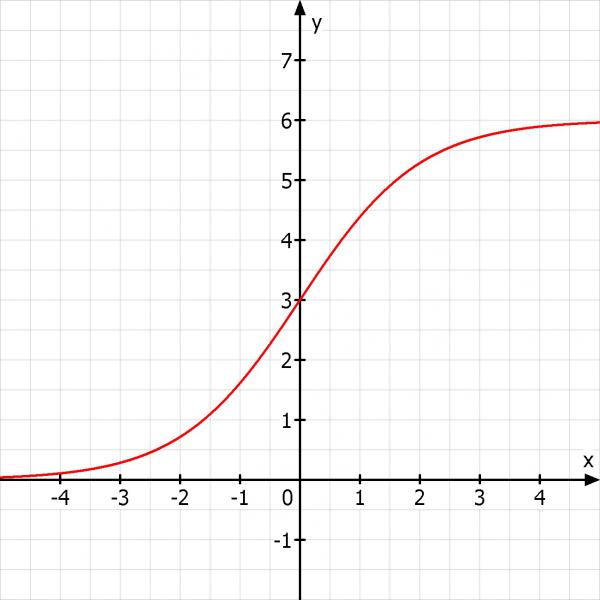
f(x) = 6/(1 + e^-x)

f '(x) = 6·e^x/(e^x + 1)²

f ''(x) = 6·e^x·(1 - e^x)/(e^x + 1)³

Und vielleicht noch eine Skizze der Funktion

Answer 2

$$ f(x) = \frac { 6 }{ 1+{ e }^{ -x } } $$

1+ e^-x = 0

e^-x = -1  ← hat keine Lösung, da e^{egal was} immer > 0

Also D = ℝ.