Kreuzen sich die beiden Flugbahen?

Question

Aufgabe

Die Flugbahn zweier Flugzeuge lautet:

F1: (20 15 10) +r (12 4 3)

F2: (-10 15 15) + s (-5 20 -4)

Kreuzen sich die beiden Flugbahen?

Problem/Ansatz

Ich habe herausgefunden, dass sich die Flugbahnen im Punkt P( -100/13| 75/13| 40/13) kreuzen.

In der Lösung steht: die beiden Flugbahn kreuzen sich bei X1=-100/13 und x2= 75/13, wobei die Flugbahn F2 mit X3=219/13 höher verläuft als die von F1 mit X3= 40/13.

Wie ist das zu verstehen, dass die Flugbahn höher verläuft, dann wären die Geraden doch windschief zueinander? Und wie kommt man rechnerisch auf diesen Wert x3= 219/13?

Answer 1

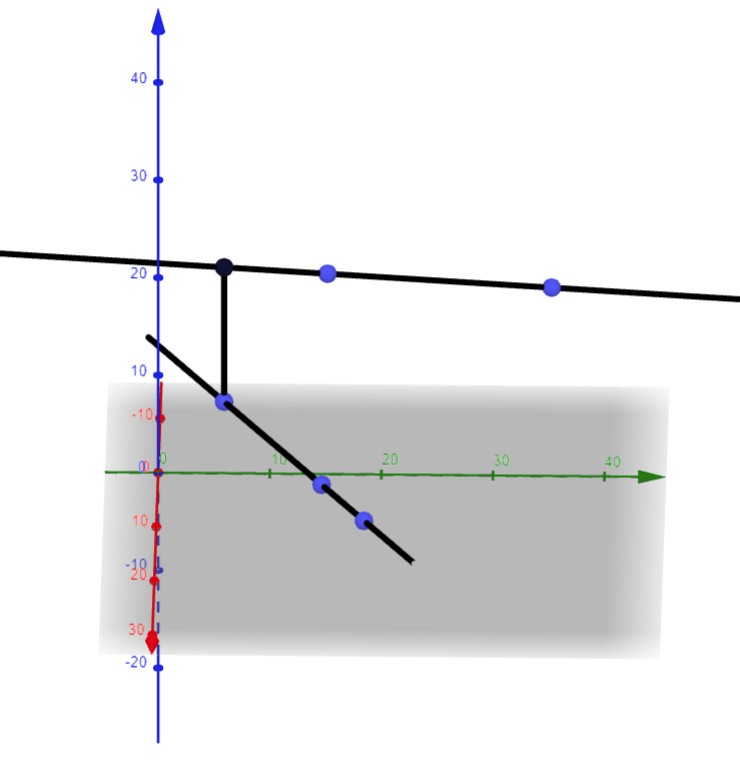
Die Geraden sind windschief. Mach doch mal eine Probe

[20, 15, 10] - 30/13·[12, 4, 3] = [- 100/13, 75/13, 40/13]

[-10, 15, 15] - 6/13·[-5, 20, -4] = [- 100/13, 75/13, 219/13]

Beide Fluggraden verlaufen über dem Punkt (- 100/13 | 75/13) eines zweidimensionalen Koordinatensystems, allerdings in unterschiedlicher Flughöhe. Die Geraden sind damit windschief.

Skizze