Eine ganzrationale Funktion 4. Grades berührt im Koordinatenursprung die x-Achse und hat bei \( x=4 \) eine Nullstelle und bei \( (2 \mid 16) \) ein lokales Maximum.
\(f(x)=a*x^2*(x-4)*(x-N)\)
\( (2 \mid 16) \):
\(f(2)=a*2^2*(2-4)*(2-N)=-8a*(2-N)\)
\(-8a*(2-N)=16\)
\(a*(N-2))=2\) \(a=\frac{2}{N-2}\)
\(f(x)=\frac{2}{N-2}*x^2*(x-4)*(x-N)\)
\(f(x)=\frac{2}{N-2}*[(x^3-4x^2)*(x-N)]\)
Bei \( (2 \mid 16) \) ein lokales Maximum:
\(f´(x)=\frac{2}{N-2}*[(3x^2-8x)*(x-N)+(x^3-4x^2)]\)
\(f´(2)=\frac{2}{N-2}*[(3*2^2-8*2)*(2-N)+(2^3-4*2^2)]=0\)
\(N=4\) \(a=\frac{2}{4-2}=1\)
\(f(x)=x^2*(x-4)*(x-4)\)
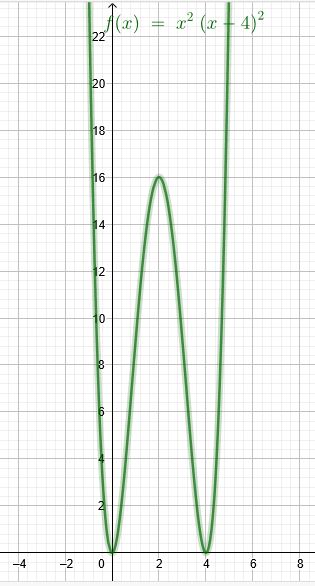
\(g_a(x) = x^4 - 8x^3 + ax^2\)
\(x^2*(x-4)^2=x^4 - 8x^3 + ax^2\)
\(x^4-8x^3+16x^2=x^4 - 8x^3 + ax^2\)
\(a=16\)