Milliliter -Einteilung im Kegel mit Hilfe des Strahlensatzes

Question

hallo ich hab ein riesen problem ich muss eine hausarbeit machen und mir fällt eine formel nicht ein:

es geht darum einen kegel zu basteln der das volumen von 800ml (800cm3) beinhaltet. ich habe mir nun folgende Werte ausgesucht

radius = 7

höhe = 15,5

durchmesser = 14

 

jetzt muss ich alle 100ml stricheinteilungen machen. und brauch hierfür die formel. (man muss den 2. strahlensatz für diese aufgabe anwenden.)

bitte helft mir ich bin echt meega am verzweifeln

Answer 1

V = 1/3 * pi * r^2 * h = 1/3·pi·7^2·15.5 = 795.3

Der Kegel würde nicht das Volumen von 800 ml fassen können. Du solltest daher entweder Radius oder Höhe etwas erhöhen.

Nimm mal einen Kegel der an der Höhe h den Durchmesser h/2 hat also den Radius von h/4

Dann errechnen sich das Volumen mit

V(h) = 1/3 * pi * (h/4)^2 * h = pi/48·h^3

h(V) = 3.Wurzel(48/pi·V)

h(100) = 11.51764764

h(200) = 14.51132671

h(300) = 16.61132236

h(400) = 18.28312598

h(500) = 19.69490043

h(600) = 20.92895471

h(700) = 22.03246733

h(800) = 23.03529529

Dieses sind also die Höhen an der jeweiligen Füllmenge. Der Kegel muss damit insgesamt etwas höher als 23 cm haben.

Comments

Eine kleine Frage: was ist mit V(h) und H(v) gemeint?

---

V(h) ist das Volumen in Abhängigkeit von der Füllhöhe h.

h(V) ist die Füllhöhe h in Amhängigkeit vom Volumen V. Also eigentlich nur die Umkehrfunktion von V(h).

---

Wäre diese Formel dann richtig?

Ich habe Höhe = 23, 5

Radius = 5,9

Durchmesser = 11,8

V(h) = 1/3*pi*5,9^2*h

---

Das wären dann 856,6 ml. Damit hat der Kegel ein größeres Volumen als 800 ml.

---

Mir ging es erstmal um den Kegel. Der kann größer als 800 ml sein. Ist wie bei Messbechern. Deren Fassungsvermögen ist ja auch etwas größer als 1000 ml. Nur wie berechne ich jetzt genau die einzelnen Abschnitte der Skala?

---

Das habe ich doch oben vorgemacht.

Es gibt zu jeder Füllmenge V eine Füllhöhe h. Diese Füllhöhe h kann mann dann ausrechnen und die dann auf dem Kegel anbringen.

Wenn man die Skala auf der Seitenlinie s anbringt kann man das nach dem Pythagoras oder Strahlensatz errechnen.

bei mit oben würde ich also rechnen

s = √(h^2 + (h/4)^2) = √17/4·h

⎡  0        0      ⎤
⎢ 100  11.87211945 ⎥
⎢ 200  14.95793320 ⎥
⎢ 300  17.12255917 ⎥
⎢ 400  18.84581490 ⎥
⎢ 500  20.30103869 ⎥
⎢ 600  21.57307273 ⎥
⎢ 700  22.71054750 ⎥
⎣ 800  23.74423890 ⎦

Das sind dann die Längen die Außen auf dem Kegel abzutragen sind.

Wir brauchen also zum Basteln einen Kreis mit dem Radius von 23,74 cm

---

Wieso mit dem Radius? Ich dachte mit der Höhe. Und muss man nicht aus dem Kreis einen Teil heraus schneiden, um einen Kegel zu basteln?

---

Ja. Du musst aus dem Kreis ein Teil herausschneiden.

Und dann bildet der Kreis ja den Mantel des Kegels und somit ist der Radius des Kreises gleichzeitig die Seitenlinie s des Kegels.

---

Also ist die Seitenlinie s 23, 74 cm lang. wie groß ist der winkel des stückes, das ich aus dem kreis rausschneiden soll? und was bedeutet in deinen Gleichungen die 48? also was hast du da gerchnet und zusammengefasst, um auf 48 zu kommen?

---

Ich habe die Formel doch nur vereifacht

V(h) = 1/3 * pi * (h/4)^2 * h = 1/3 * pi * h^2 / 16 * h = pi/48·h^3

Da s = 23,74 cm lang sein muss ist der Umfang

U = 2 * pi * r = 149,2 cm

Unser entstehender Gegel hat an der Grundfläche den radius von h/4 also

h/4 = 23,04 / 4 = 5,76 cm

Das gibt einen Umfang von

U2 = 2 * pi * r = 36,19 cm

Damit ist unser Sektorwinkel 36,19 / 149,2 * 360 = 87,32 Grad

Ich hoffe das Stimmt so. Also versuchsweise mal so basteln und schauen obs stimmt.

Wenn beim ausleeren einer 1 l Milchpackung 200 ml überschwappt, dann scheint es richtig zu sein :-)

---

Jetzt hab ich alles verstanden :) nur wie kommst du auf 48? Ich hab vieles durch probiert, aber bin nie drauf gekommen. Also aus was setzen die sich zusammen?

Answer 2

Du müsstest die Länge der Kante haben, um mal einen Kreis zu zeichnen. Dort muss man dann ein Teil wegschneiden, den man vom Gezeichneten Kreis wegschneidet. Ich rechne mal dies aus:

Um die Kante auszurechnen, kann man den Pythagoras verwenden:

√(7²+15.5²)=x

x≈17.00735135cm

 

Dies ist also der Umfang des Kreises, den du zeichnen musst.

 

Und nun zum 2. Teil:

Von dem kannst du den Umfang berechnen und den Umfang der Grundfläche des Kegels zu subrtahieren. Dieses Teilstück gibt dann den Winkel beim Mittelpunkt, den die auzuschneidende Fläche hat (achtung: Klebelaschen nicht vergessen):

U_Zeichnung=2xπ=2*17.00735*π= 106.86034401

U_{Grundfläche Kegel}=14*π=43.98229715

U_z : U_G = β : 360 = 106.86034401 : 43.98229715

β = 43.98229715 * 360 / 106.86034401 = 148.1712201°

α = 360° - β = 211.8287799° 

 

Du musst ein Dreieck mit dem Zentriwinkel von 212° ausschneiden (und fortwerfen, Klebelaschen nicht vergessen). Hier mal noch 'ne Grafik dazu:

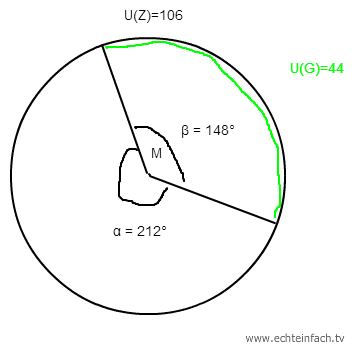
Jetzt muss man noch die Höhe der 100 ml einzeichnen: 

Du machst eine Hilfslinie von M aus und trägst dort 8 gleichlange Stücke ab (Länge egal, sollte jedoch aufs Blatt passen). Nun verbindest du den am weitesten entfernten Punkt mit der Ecke. Jetzt einfach noch die parallelen dazu durch die Teilstücke abtragen, und nun mit dem Zirkel bei M einstechen, Linien (Kreisbögen) durchziehen:

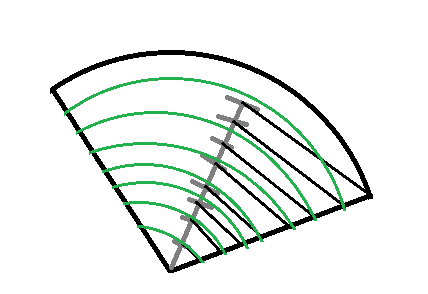
...und Zusammenkleben - Fertig.

 

Ich hoffe, ich konnte helfen und du verstehst es nun!

Simon

Comments

Ich sehe gerade, die Masse stimmen nicht (Ich habe deine Masse übernommen).... einfach Zahlen anpassen (in die Richtigen Werte ändern) und weiter....

---

Du machst eine Hilfslinie von M aus und trägst dort 8 gleichlange Stücke ab (Länge egal, sollte jedoch aufs Blatt passen)

Die Einteilung darf nicht linear oder gleichmäßig sein, da in eine Kegelspitze bei gleicher Füllhöhe weniger Flüssigkeit geht als am Kegelboden.

---

uups, stimmt!

kann man denn den Strahlensatz auch anders anwenden (hier)? Mir fällt so nichts ein!