Ein Händler bietet zehn Flaschen „süßen Wein" zum Sonderpreis an, obwohl er weiß, dass in vier Flaschen der Inhalt bereits vergoren und sauer ist. Ein Kunde will die zehn Flaschen kaufen, probiert aber vorher den Inhalt zweier Flaschen. Wie groß ist die Wahrscheinlichkeit, dass der Kunde den Betrug bemerkt?
Der Betrug fliegt auf wenn mind. eine Flasche vergorenen Wein erhält. Der Betrug fliegt nicht auf wenn beide Flaschen in Ordnung sind.
P(Betrug wird bemerkt) = 1 - P(Betrug wird nicht bemerkt) = 1 - 6/10 * 5/9 = 2/3
Zu 2/3 = 66.67% wird der Betrug also vom Kunden bemerkt.
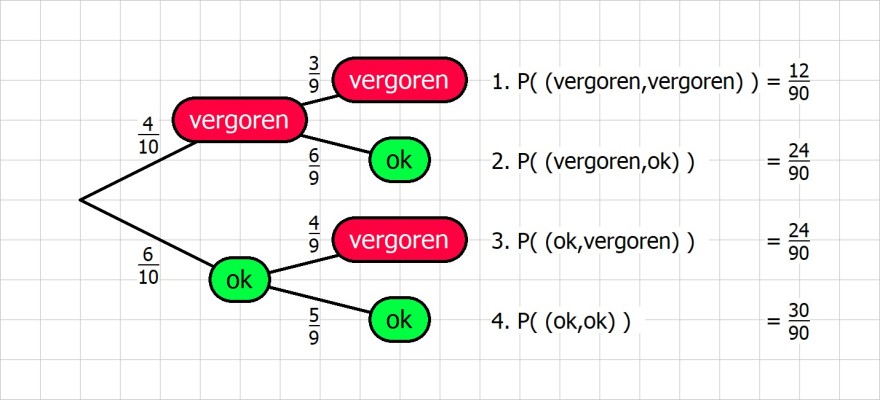
Ein Baumdiagramm kann helfen.