Aufgabe:
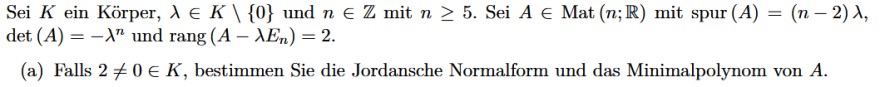
Text erkannt:
Sei \( K \) ein Körper, \( \lambda \in K \backslash\{0\} \) und \( n \in \mathbb{Z} \) mit \( n \geq 5 \). Sei \( A \in \operatorname{Mat}(n ; \mathbb{R}) \) mit spur \( (A)=(n-2) \lambda \), \( \operatorname{det}(A)=-\lambda^{n} \) und \( \operatorname{rang}\left(A-\lambda E_{n}\right)=2 \).
(a) Falls \( 2 \neq 0 \in K \), bestimmen Sie die Jordansche Normalform und das Minimalpolynom von \( A \).
Problem/Ansatz:
Kann mir jemand sagen wo ich anfangen soll? :D