Grenzwert rekursiver Folgen berechnen

Question

Aufgabe:

Problem/Ansatz:

Hallo zusammen,

ich sitze gerade an dieser Aufgabe und habe leider ein paar Verständnisprobleme.

Angefangen bei der 1:

Ich verstehe nicht , warum hier mehrere Grenzwerte für (an) verlangt werden. Aus meiner Sicht gibt es hier nur 1 unzwar 7??

da für x gegen unendlich, der Ausdruck \( \frac{10}{x} \) gegen 0 strebt und somit 7 bleibt.

Oder sind hier die möglichen Grenzwerte für die folge (an+1) gemeint?

Nun zur 2:

Ich habe die Tabellenkalkulation gemacht:

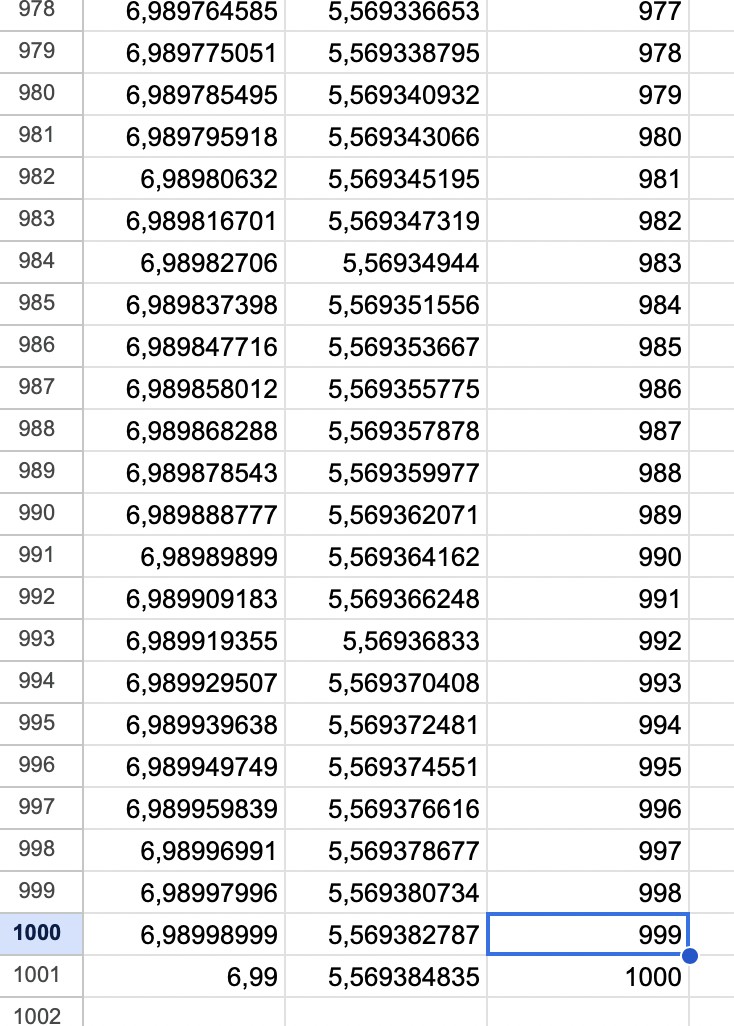
Hier strebt (an) für n gegen unendlich gegen 7 und (an+1) gegen 5,57143 bzw. \( \frac{39}{7} \), da Lim(an) = 7.

=> Lim(an+1) = 7- \( \frac{10}{7} \) = \( \frac{39}{7} \)

Aufgabe 3:

Verstehe ich leider überhaupt nicht, denn wie ich bereits erwähnt habe, verstehe ich nicht ganz, warum hier mehrere Grenzwert verlangt werden.

Es kann gut sein, dass ich die Aufgabe überhaupt nicht richtig verstanden habe.

Ich bin für jede Hilfe dankbar!

Comments

Ich komme auf 5 als Grenzwert?

Answer 1

Zu 1.:

Sei \((a_n)\) konvergent gegen \(a\), dann ist auch

\((a_{n+1})\) konvergent gegen \(a\), da Teilfolge.

Wegen der Stetigkeit von \(f(x)=7-\frac{10}{x}\)

für \(x\neq 0\) hat man dann

\(a=\lim a_{n+1}=\lim (7-\frac{10}{a_n})=7-\frac{10}{\lim a_n}=7-\frac{10}{a}\).

Das bedeutet \(0=a^2-7a+10=(a-2)(a-5)\).

Mögliche Grenzwerte sind also \(2\) und \(5\).