Skizze machen:
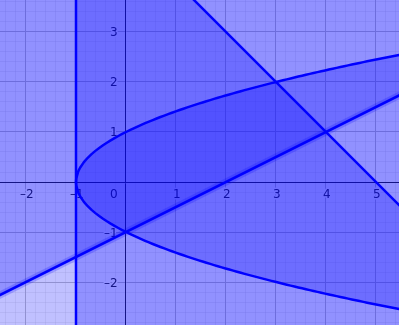
Dann musst du dich entscheiden ob du im äußeren Integral über x oder y integrieren willst. Ich wähle hier y, da man so nur 2 Teilintegrale enthält. Also schreibt man mal hin:
$$ \iint_B f(x,y) ~\textrm dA = \int_{-1}^2 \int_{u(y)}^{o(y)} f(x,y) ~\textrm dx \textrm dy $$
Jetzt muss man noch die Grenzen für das x-Integral bestimmen. Dazu formst du die Ungleichungen am besten in die Form:
$$ x \le ... \quad \text{oder}\quad ...\le x $$
um. Ungleichungen erster Form liefern dir obere Grenzen, Ungleichungen zweiter Form untere Grenzen. Man findet
$$ u(y) = y^2 - 1 $$ $$ o(y) = \begin{cases} 2y+2 & y \le 1\\5-y & y \ge 1\end{cases} $$
Also
$$ \iint_B f(x,y) ~\textrm dA = \int_{-1}^1 \int_{y^2-1}^{2y+2} f(x,y) ~\textrm dx \textrm dy + \int_{1}^2 \int_{y^2-1}^{5-y} f(x,y) ~\textrm dx \textrm dy $$