Wenn die tatsächliche Gewinnwahrscheinlichkeit 7% beträgt?

Question

Aufgabe:

Ein Losverkäufer behauptet, dass jedes zehnte Los gewinnt. Wir wollen ihn durch einen Binomialtest zum Signifikanzniveau alpha=0.05 nachweisen, dass er die Gewinnwahrscheinlichkeit zu hoch angibt. Die unbekannte Gewinnwahrscheinlichkeit pG soll also mit der Refernzwahrscheinlichkeit p0=0.1 verglichen werden. Wir kaufen 198 Lose.

Was ist die Power des Tests. Wenn die tatsächliche Gewinnwahrscheinlichkeit 7% beträgt?

Problem/Ansatz:

Ich bekomme am Ende 0.44433 raus, was leider falsch ist.

Dazu Lautet die Nullhypothese H0={pG>0.1} falls das relevant ist.

Vielen Dank schonmal im Voraus für eine Antwort :)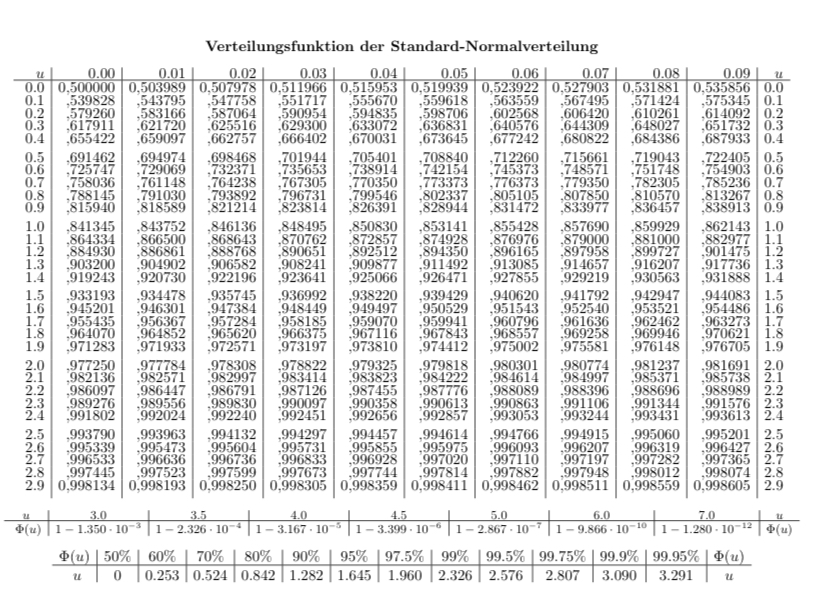

Text erkannt:

Verteilungsfunktion der Standard-Normalverteilung
\begin{tabular}{c|c|c|c|c|c|c|c|c|c|c|c|c|c}
$\Phi(u)$ & $50 \%$ & $60 \%$ & $70 \%$ & $80 \%$ & $90 \%$ & $95 \%$ & $97.5 \%$ & $99 \%$ & $99.5 \%$ & $99.75 \%$ & $99.9 \%$ & $99.95 \%$ & $\Phi(u)$ \\
\hline$u$ & 0 & 0.253 & 0.524 & 0.842 & 1.282 & 1.645 & 1.960 & 2.326 & 2.576 & 2.807 & 3.090 & 3.291 & $u$
\end{tabular}

Answer 1

Wie kommst du denn genau auf deine Wahrscheinlichkeit? Ich komme auf

P(X ≤ 12 | p = 0.07) = 0.3656

Comments

Ich habe (14-198*0.07/Wurzel(198-0.07*(1-0.07)) ausgerechnet daraus kommt 0.147121 raus.

Wenn man dann in die Tabelle guckt kriegt man den Wert 0.555670 (0.1 links am rand dann 0.04 oben).

Das habe ich dann 1-0.555670 gerechnet, woraus 0.44433 rauskommt.

---

Hey nochmal!

Könnten sie vielleicht den ganzen Rechenweg den sie angewendet haben erläutern ?

---

Wie kommst du auf deine 14. Wie du meinem Ansatz entnehmen kannst habe ich mit 12 statt 14 gerechnet. Achso. Ich habe keine Näherung über die Standardnormalverteilung gemacht.

---

Ich bin eigentlich auf auf ca 12 gekommen aber das Programm hatte aus irgendeinem Grund nur 14 akzeptiert, wieso genau weiß ich leider auch nicht.

---

Also mit 14 lautet die rechnung wie folgt:

1 - NORMAL((14 - 198·0.07)/√(198·0.07·0.93))
= 1 - NORMAL(0.14/3.590)
= 1 - NORMAL(0.03899)
= 1 - 0.5156
= 0.4844

---

Danke für die Antwort!