Aufgabe:
Problem/Ansatz:
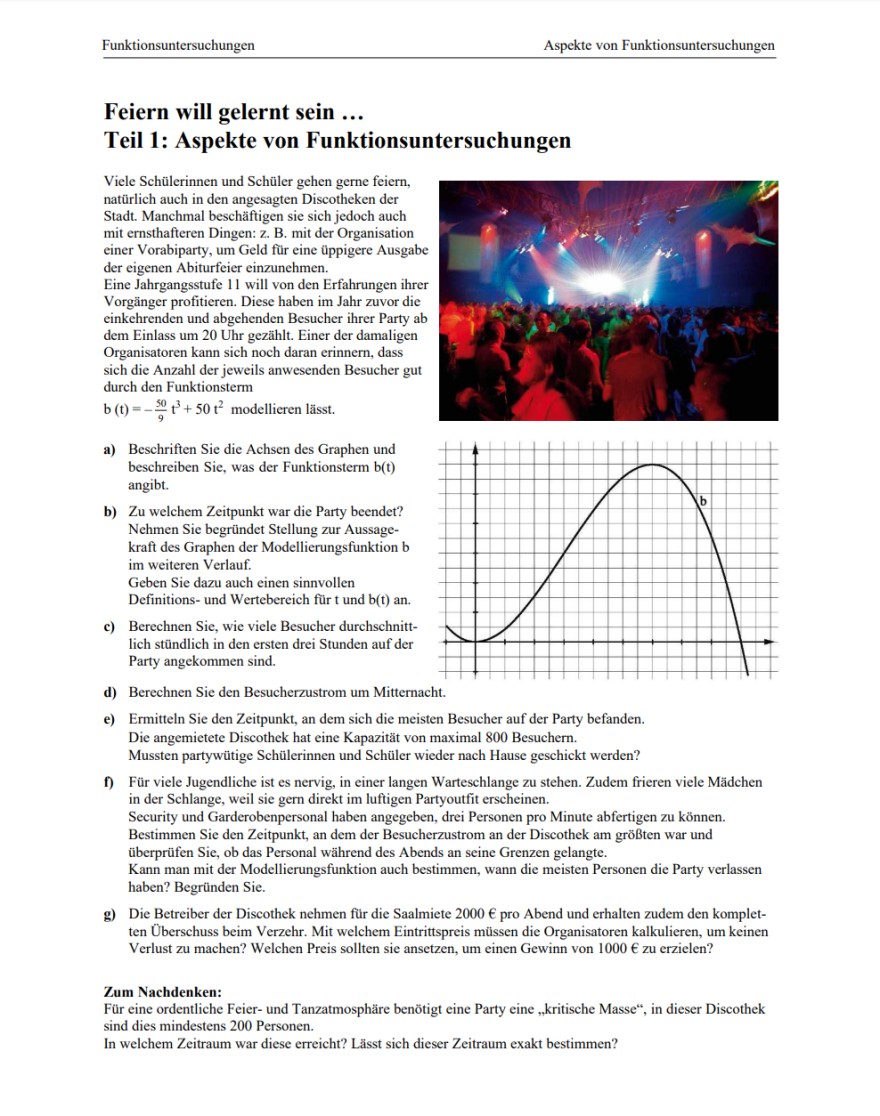
Bei e)
Um den Zeitpunkt zu ermitteln, an dem sich die meisten Besucher auf der Party befanden, müssen wir den Wert von t finden, für den b(t) maximal ist. Das bedeutet, wir müssen das Maximum des Funktionsterms b(t) finden. Dazu können wir Ableitungen verwenden. Indem wir den Funktionsterm ableiten und die Ableitung gleich null setzen, finden wir den kritischen Punkt. Wenn die zweite Ableitung an dieser Stelle negativ ist, handelt es sich um ein Maximum.
Um das Maximum von b(t) zu finden, nehmen wir die Ableitung des Funktionsterms:
b'(t) = d/dt (-50/9)t^3 + 50t^2
Um den kritischen Punkt zu finden, setzen wir die Ableitung gleich null:
0 = -150/9t^2 + 100t
Um diese Gleichung zu lösen, multiplizieren wir sie mit 9, um den Bruch zu eliminieren:
0 = -150t^2 + 900t
Nun faktorisieren wir die Gleichung:
0 = 150t(6 - t)
Daraus ergeben sich zwei Lösungen:
t1 = 0
t2 = 6
Da wir den Zeitpunkt vor dem Einlass (t = 0) ausschließen können, ist der Zeitpunkt, an dem sich die meisten Besucher auf der Party befanden, t = 6 Stunden.
Um herauszufinden, ob partywütige Schülerinnen und Schüler nach Hause geschickt werden mussten, prüfen wir, ob zu irgendeinem Zeitpunkt die Anzahl der Besucher die maximale Kapazität von 800 überschritten hat. Wir überprüfen also den Funktionsterm b(t) für alle Werte von t:
b(t) = -(50/9)t^3 + 50t^2
Wenn es einen Wert von t gibt, für den b(t) größer als 800 ist, mussten Schülerinnen und Schüler abgewiesen werden.
Ist das soweit korrekt?