um das oben schon angedeutet fortzuführen, habe ich mich etwas in das 'neue' Desmos-Geometry eingearbeitet:
diesmal ist es (noch) nicht interaktiv, man muss auf den Link kllicken.
https://www.desmos.com/geometry-beta/jdhno9xwtk
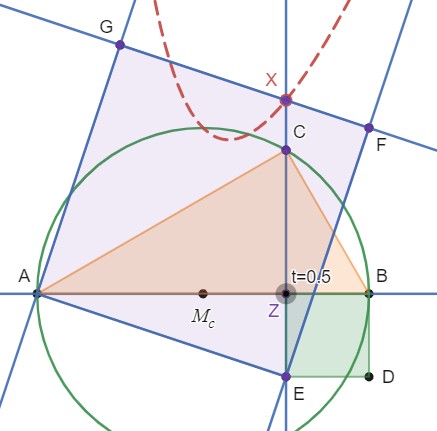
oben sieht man das rechtwinklige Dreieck \(ABC\) aus der Originalaufgabe. Die Vierecke \(AEFG\) und \(EDBZ\) sind Quadrate. Die Frage ist nun unter welchen Bedingungen der Punkt \(C\) auf der Geraden durch \(FG\) liegt. (s. auch Kommentar von hj2166)
Dazu konstruiere ich - bei gegebenen Dreieck \(ABC\) - das Quadrat \(EDBZ\) und anschließend das Quadrat \(AEFG\). Der Schnittpunkt der Geraden durch \(FG\) und der Verlängerung der Höhe \(h_c\) alias Gerade durch \(CZ\) sei \(X\). Durch horizontales Verschieben von \(Z\) auf \(AB\) bildet sich die Ortskurve von \(X\) (rot gestrichelt).
Die beiden Schnittpunkte dieser Ortskurve mit dem Tahleskreis (grün) über \(AB\) sind die Punkte bei denen \(C\) auf \(FG\) liegt.
Die Ortskurve von \(X\) ist eine Hyperbel. Ist der Thaleskreis der Einheitskreis in einem Koordinatensystem und liegt \(B\) auf der positiven X-Achse, so ist diese Hyperbel der Graph der Funktion$$f(x) = 3x-3 + \frac{4}{x+1}$$Der linke Schnittpunkt liegt dann etwa bei \(x\approx 0,274\)