Ich habe in der Schule eine Aufgabe bekommen:
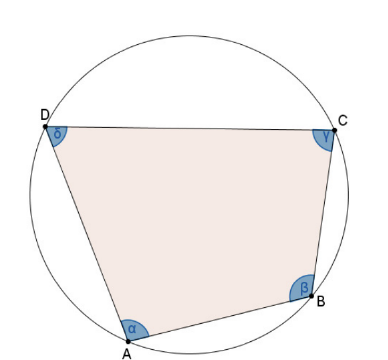
Beweise: Ist ABCD ein Viereck, bei dem alle vier Eckpunkte auf demselben Kreis liegen, dann gilt Winkel CBA + Winkel ACD = 180°. Ein solches Viereck heißt Sehnenviereck.
Unterscheide die folgenden drei Fälle:
Fall 1: Der Mittelpunkt des Umkreises k liegt im Inneren des Vierecks ABCD.
Fall 2: Der Mittelpunkt des Umkreises k liegt außerhalb des Vierecks ABCD.
Fall 3: Der Mittelpunkt des Umkreises k liegt auf einer Seite des Vierecks ABCD.
Der Satz ist äquivalent zum Peripheriewinkelsatz.
Dieser soll hier zum Beweis nicht verwendet werden.
Ich habe den ersten Fall ziemlich einfach Lösen können:
(ich weiß nicht ob latex hier funktioniert aber mal sehen)
Behauptung:
In einem Sehnenviereck ist die Summe der Größen gegenüberliegender
Innenwinkel stets 180°. Daraus folgt, dass
\(\alpha + \beta = 180{^\circ}\) und
\(\beta + \gamma = 180{^\circ}\) gilt.
Beweis:
Ich werde zuerst das Sehnenviereck betrachten in welchem der Mittelpunkt
innerhalb des Vierecks ist. Ich ziehe von dessen Mittelpunkt {\(M\)}
Verbindungslinien zu den Eckpunkten und jetzt entstehen vier
gleichschenklige Dreiecke \(AMB\), \(BMC\),\(CMD\) und \(DMA\).
Die langen Schenkel von ihnen haben immer die länge \(r\) (Radius des
Umkreis) haben.
Daraus wird gefolgert, dass die zugehörigen Basiswinkel in jedem dieser
Dreiecke gleich groß sind:\\
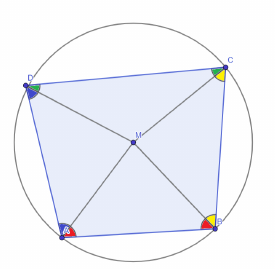
\(\angle MAB = \angle MBA = rot\)
{\(\angle MBC = \angle MCB = gelb\)};\\
{\(\angle MCD = MDC = gruen\)};\\
{\(\angle MDA = \angle MAD = blau\)}
Aus der Abbildung kann man ablesen, dass die Winkelsumme im
Sehnenviereck aus {\(2(rot + gelb + gruen + blau) = 180{^\circ}\)}
ist.\\
Dies ist die Summe zweier gegenüberliegender Innenwinkel.\\
Die Behauptung wurde bewiesen, da CBA und ADC gegenüberliegen.
Das war meine Lösung dafür. Aber bei den nächsten beiden besonders bei dem wo der Mittelpunkt außerhalb des Vierecks liegt komme ich einfach nicht weiter. Kann mir da jemand helfen?