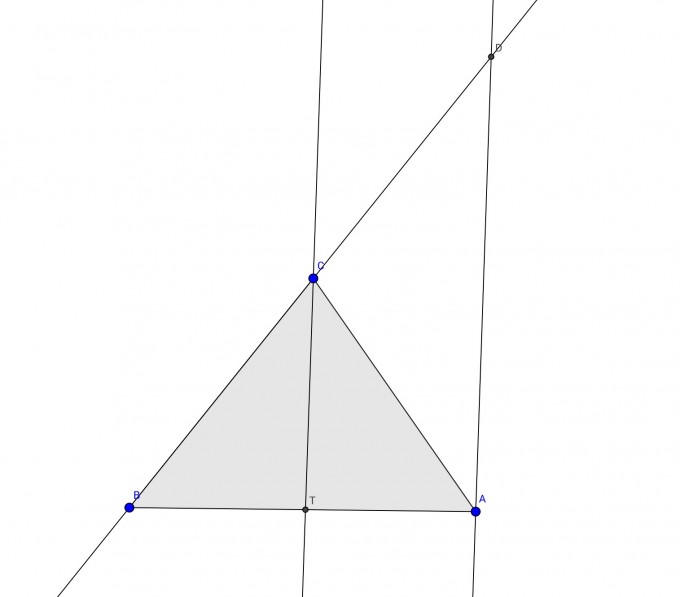
Ich habe das Dreieck ABC gegeben. T ist der Schnittpunkt der Winkelhalbierenden durch C mit der gegenüberliegenden Seite. Daraus folgt, dass ΙATI / IBTI = IACI / IBCI.
Um das zu beweisen habe ich erst einmal einen Punkt D konstruiert, in dem ich die Parallele zu CT durch A kostruiert habe und diese dann mit der Gerade durch BC geschnitten habe. Dann kann man ja den Strahlensatz anwenden, weil ich zwei parallele Geraden habe und das Zentrum B.
Dadurch komme ich dann auf IATI / IBTI = IDCI / IBCI. Also muss ich ja nur noch zeigen, dass DC=AC ist. Anschaulich ist das klar, aber wie begründe ich das? Muss ich das mit ähnlichen Dreiecken machen oder kann man das anders begründen? Und reicht das als Beweis oder muss ich da anders vorgehen?
Vielen Dank an alle Helfenden! :)