Aufgabe:
Gegeben sei folgender Digraph \( G=(V, A) \), dessen Pfeile \( a \in A \) im linken Bild mit den KapazitätenKosten-Tupeln \( (u(a), c(a)) \) und im rechten Bild mit Flusswerten \( f(a) \) beschriftet sind:
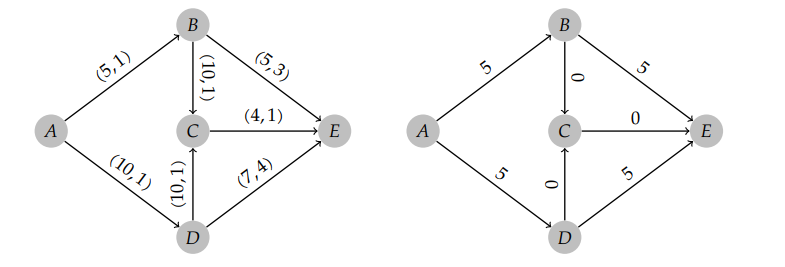
Problem/Ansatz:
2.1 Für welches \( b: V \rightarrow \mathbb{R}_{+} \)ist der Fluss \( f \) auf der rechten Seite ein \( b \)-Fluss?
\( (5 \)
2.2 Führen Sie per Hand den Cycle-Cancelling-Algorithmus durch, um ausgehend von dem
\( (4 \) Fluss \( f \) einen \( b \)-Fluss auf \( (G, u, b, c) \) mit minimalen Kosten zu bestimmen.