Länge einer Sehne (Zweikreisfigur)

Question

Zwei sich berührende Kreis K₁ und K₂ haben beide den Radius 3·√2 und ihre Mittelpunkte liegen auf einem in A beginnenden Strahl. A liegt außerdem auf K₁. Aus der Tangente durch A an K₂ scheidet K₁ einen Abschnitt heraus, dessen Länge zu berechnen ist.

Answer 1

Nach Pythagoras gilt

x^2 = (3·3·√2)^2 - (3·√2)^2 --> x = 12 (Strecke AC)

Nach Strahlensatz gilt

y / (2·3·√2) = (12) / (3·3·√2) --> y = 8 (Strecke AB)

Für die grüne Strecke nach Moliets gilt

y / (3·√2) = (12) / (3·3·√2) --> y = 4 (Strecke BC)

Skizze

Comments

Mathecoach: Leider tauchen deine Benennungen x und y in deiner Skizze nicht auf.

---

Ebenso fehlt in meiner Skizze auch das Dreieck in dem ich den Pythagoras anwende.

Ich erwarte also meist schon ein klein wenig Mitdenken der Leser.

Aber für die, die mit der Bezeichnung x, y nichts anfangen können, habe ich das jetzt noch in der Rechnung dahinter geschrieben, welche Strecken das in der Zeichnung sind.

Answer 2

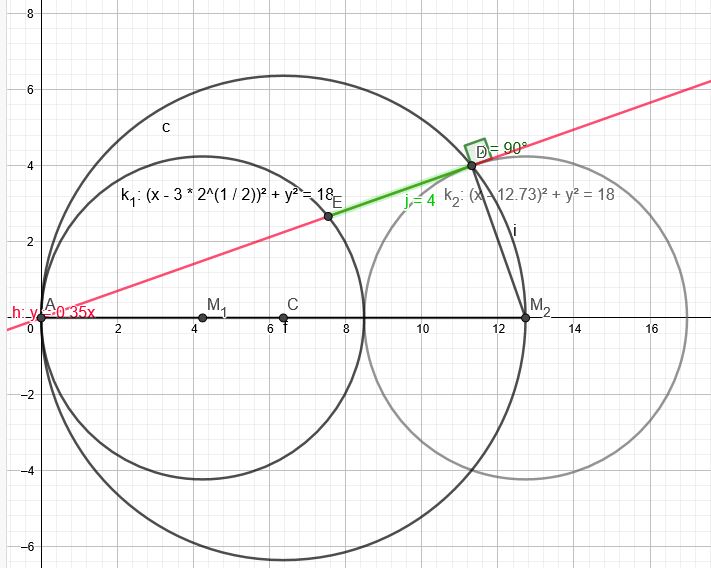
1.) \(A(0|0)\)

2.) \(M_1(3*\sqrt{2}|0)\)

3.) Kreis um 2.): \((x-3*\sqrt{2})^2+y^2=18\)

4.) \(M_2(3*3*\sqrt{2}|0)\)

5.) Kreis um 4.): \((x-3*3*\sqrt{2})^2+y^2=18\)

6.) Mitte der Strecke A M_2   \(C(1,5*3*\sqrt{2}|0)\)

7.) Thaleskreis um 6.) \((x-1,5*3*\sqrt{2})^2+y^2=(1,5*3*\sqrt{2})^2=40,5\)

Der Thaleskreis schneidet k_2 in \(D(11,31|4)\)

Tangente durch A und D schneidet k_1  in \(E(7,54|2,67)\)

Länge DE:\( \sqrt{(4-2,67)^2+(11,31-7,54)^2}=4 \)

Comments

@Moliets: wie stehst Du eigentlich zum Thema Ästhetik in der Mathematik?

---

Bist du sicher, dass in der Aufgabe nach der grünen Strecke gefragt wird? Ich lese das etwas anders.