Aufgabe:
Auflösen einer Funktionsgleichung mit bekanntem Endergebnis
Problem/Ansatz:
Ich stehe gerade vor einem mathematischen Problem, das ich nicht lösen kann aus aktueller Sicht und bitte um Hilfe:
Mir stehen 2. verschiedene Basisformeln zur Verfügung. Das Endergebnis müsste lt. Simulation bekannt sein und wie folgt lauten:
Gy2(p) = \( \frac{1}{1+5p} \)
Basisformeln siehe bitte Anhang
Seht ihr hier einen mathematischen Weg, um auf die gewünschte Endformel zu kommen?
Danke, MfG
Text erkannt:
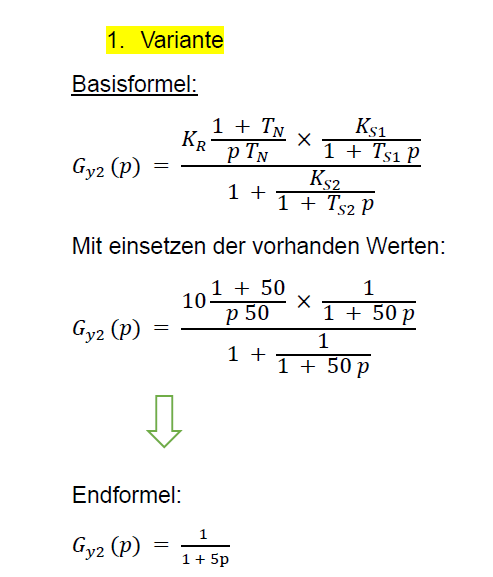
1. Variante
Basisformel:
\( G_{y 2}(p)=\frac{K_{R} \frac{1+T_{N}}{p T_{N}} \times \frac{K_{S 1}}{1+T_{S 1} p}}{1+\frac{K_{S 2}}{1+T_{S 2} p}} \)
Mit einsetzen der vorhanden Werten:
\( G_{y 2}(p)=\frac{10 \frac{1+50}{p 50} \times \frac{1}{1+50 p}}{1+\frac{1}{1+50 p}} \)
Endformel:
\( G_{y 2}(p)=\frac{1}{1+5 p} \)
Text erkannt:
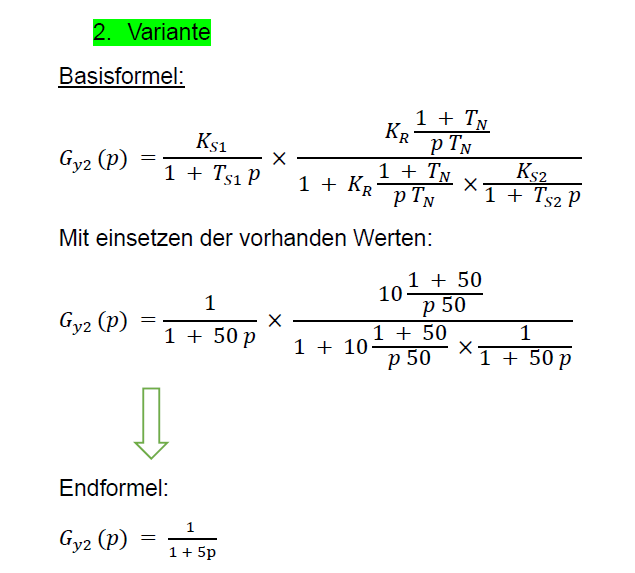
2. Variante
Basisformel:
\( G_{y 2}(p)=\frac{K_{S 1}}{1+T_{S 1} p} \times \frac{K_{R} \frac{1+T_{N}}{p T_{N}}}{1+K_{R} \frac{1+T_{N}}{p T_{N}} \times \frac{K_{S 2}}{1+T_{S 2} p}} \)
Mit einsetzen der vorhanden Werten:
\( G_{y 2}(p)=\frac{1}{1+50 p} \times \frac{10 \frac{1+50}{p 50}}{1+10 \frac{1+50}{p 50} \times \frac{1}{1+50 p}} \)
Endformel:
\( G_{y 2}(p)=\frac{1}{1+5 p} \)