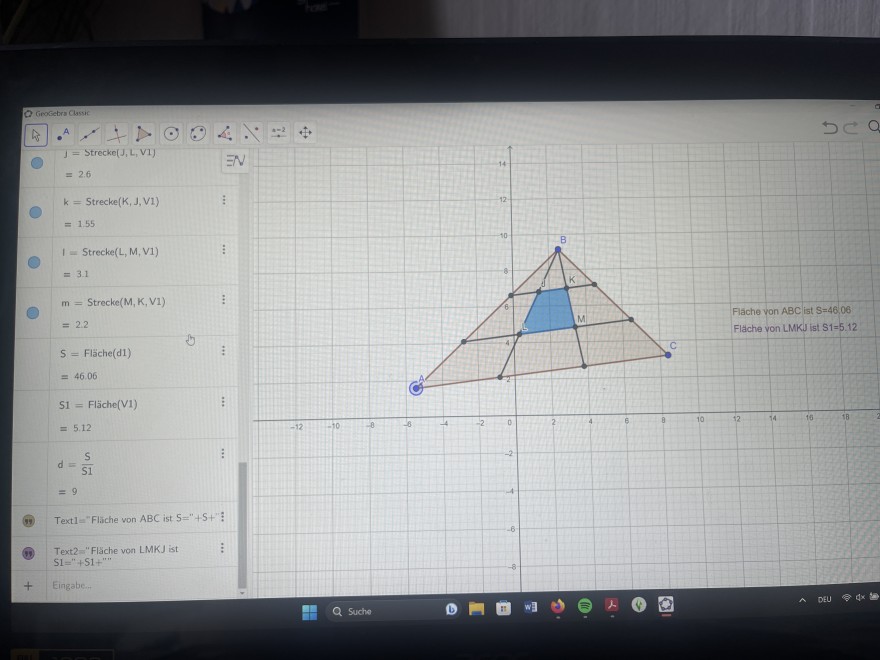
Hey, also das Dreieck habe ich soweit fertig und auch die Fläche berechnet.
Berechnen Sie die Fläche \( S \) von \( A B C \) und lassen Sie \( S \) und \( S_{1} \) als dynamischen Text anzeigen. Was können Sie über das Verhältnis zwischen der Fläche \( S \) und \( S_{1} \) sagen? Ändert es sich wenn Sie das Dreieck \( A B C \) vergrößern bzw. verkleinern oder an einem der Eckpunkte ziehen? Schreiben Sie Ihre Beobachtung als Text unter dem Dreieck auf und überprüfen Sie Ihre Hypothese mit einem wahr-falsch-Bericht.
Wie kann ich es mit dem Wahr-Falsch-Bericht machen?
Beobachtung ist, dass wenn die Fläche des Dreiecks größer/kleiner wird, auch die Fläche des Vielecks größer/kleiner.
Allerdings bleibt S/S1 immer bei ≈9