Für welche der folgenden Differentialgleichungen handelt es sich um das umskalierte Richtungsvektorfeld?

Question

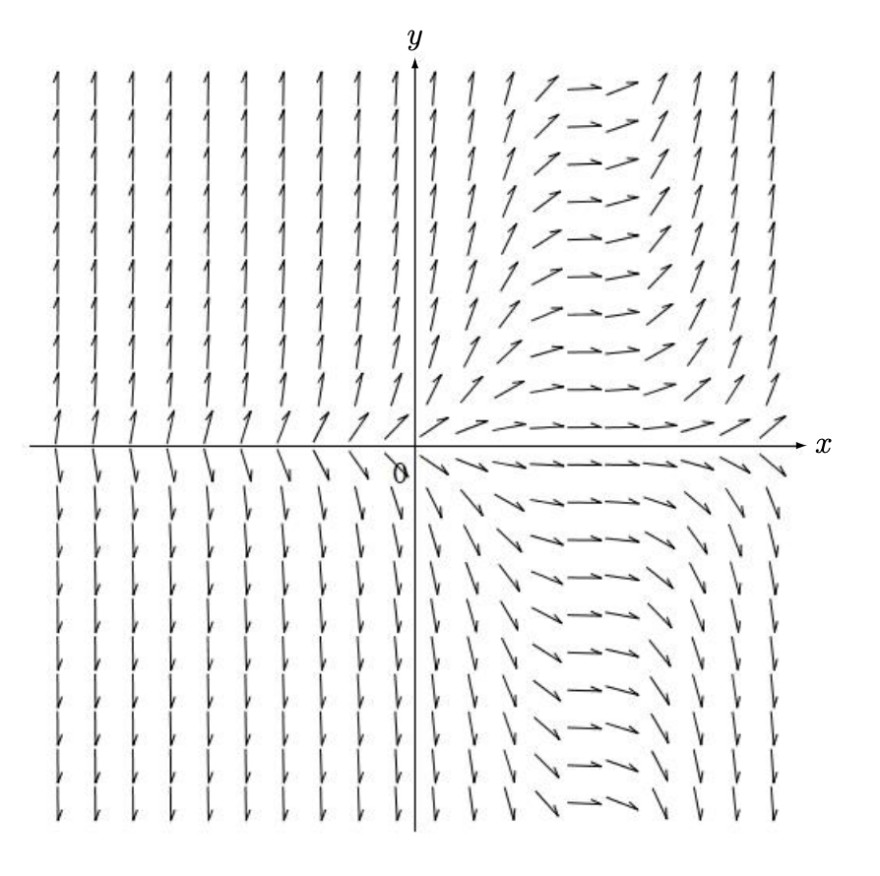
Aufgabe:

In der angehängten Abbildung sehen Sie ein umskaliertes Richtungsvektorfeld einer gewöhnlichen Differentialgleichung erster Ordnung. Für welche der folgenden Differentialgleichungen handelt es sich um das umskalierte Richtungsvektorfeld?

(A) \( f'(x) = f(x)(x - 2) \)

(B) \( f'(x) = f(x)(x - 2)^2 \)

(C) \( f'(x) = f(x)(f(x) - 1) \)

(D) \( f'(x) = f^2(x)(f(x) - 1) \)

Problem/Ansatz:

Nun, wenn wir ein x festlegen, sehen wir, dass die Vektoren auf der vertikalen Linie sich nicht verändert, bedeutet die Gleichung hängt von x ab. Somit können wir C und D ausschliessen. Aber wie entscheide ich mich zwischen A und B?

Comments

Ahh ich kann das Stabilitätstheorem anwenden, also einfach x als konstant ansehen und dann die Ableitung nach f(x) nehmen und im Equilibrium evaluieren. Für A: F'(0) = -2 < 0 also stabil, und das Equilibrium im Bild ist instabil. Für B: F'(0) = (-2)^2 = 4 > 0 instabil. Also ist B die Antwort.

Answer 1

Am einfachsten über das Vorzeichen:

z.B. y=1,x=0: A) gibt negative Steigung, B) positive. Und, wohin zeigen die Pfeilchen im Punkt (0,1), nach oben oder nach unten?

Comments

Nach oben, also B. Vielen Dank :D