In einer Aufgabe sollten 6 Differentialgleichungen 6 gegebenen Richtungsfeldern zugeordnet werden.
$$a)\quad y'x+y=0\leftrightarrow y'=-\frac{y}{x}$$
$$b)\quad yy'+x=0\leftrightarrow y' = -\frac {x}{y}$$
a) wurde dieses Richtungsfeld zugeordnet:
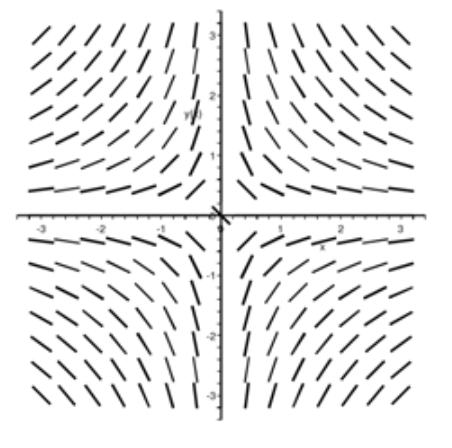
Es macht Sinn für mich, dass die y-Achse keine Tangenten enthält, weil dort x = 0 ist.
(1) Warum jedoch gibt es eine Tangente im Nullpunkt? 0/0 ist doch nicht definiert.
(2) Kann ich davon ausgehen, dass es auf der x-Achse lauter horizontale Tangenten (also Steigung = 0) hat?
b) wurde dieses Richtungsfeld zugeordnet:
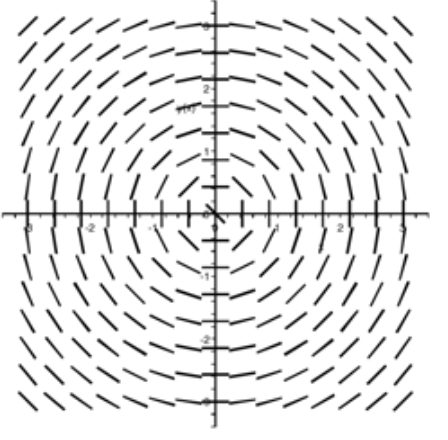
(3) Ich verstehe nicht, wieso es auf der x-Achse vertikale Tangenten hat. Für y = 0 ist doch nichts definiert. Da dürften meiner Meinung nach deshalb analog zum anderen Richtungsfeld keine Tangenten sein.