Bestimmen Sie die Stelle, wo der Wagen in die Reifen fährt: f(x) = 9-1/4x^2

Question

Die "Curva parabolica" von Monza ist eine der berüchtigsten Formel-1-Kurven. Sie ist die letzte vor der Start- und Zielgeraden und wird (im 2. Gang) mit 165 km/h durchfahren. Die Parabolica ist eine Rechtskurve.

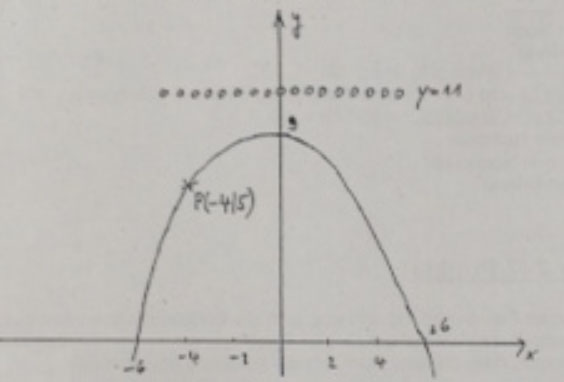
Die Funktionsgleichung \( f(x) = 9 - \frac{1}{4} x^2 \) ist eine akzeptable Annâherung des (parabelförmigen) Streckenverlaufs.

Bis zum Punkt P(-4|5) geht noch alles gut, doch dann verliert der Fahrer die Kontrolle über das Fahrzeug, fährt geradeaus weiter und landet schließlich in den aufgestapelten Reifen, die bei y=11 angebracht sind.

Bestimmen Sie die Stelle, wo der Wagen in die Reifen fährt.

Answer 1

Hi,

bestimme die Ableitung im Punkt P(-4|5)


f'(x) = -1/2x

f'(-4) = -1/2*(-4) = 2


Die Steigung im Punkt P ist also 2. Das ist damit auch die Steigung der Tangenten:

y = 2x+b

Um b zu errechnen P einsetzen:

5 = 2*(-4)+b

b = 13


Die Gerade sieht wie folgt aus: y = 2x+13

Schnittpunkt mit y = 11 bestimmen:


2x+13 = 11   |-13

2x = -2

x = -1


Der Rennfahrer wird bei Q(-1|11) auf die Absperrung treffen.


Grüße