Aufgabe:
Bestimmen der Tangente Typ A - Anwendungsaufgabe
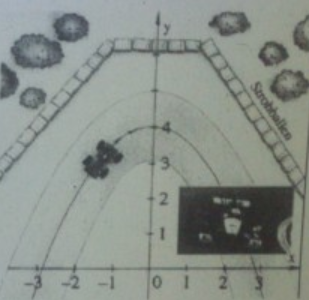
Die sogenannte „Ideallinie“ der in der Abbildung gezeichneten Kurve einer Rennstrecke wird durch eine Funktion mit dem Funktionsterm \( y(x)=4-\frac{1}{2} x^{2} \) beschrieben. Wegen zu späten Bremsens kommt der Wagen am Punkt \( \mathrm{P}(-2|…) \) von der Ideallinie ab und rutscht geradlinig in die Strohballen.
Arbeitsaufträge:
a) Bestimme zuerst zeichnerisch so genau wie möglich den Punkt Q(...|6), an dem der Wagen in die Strohballen fährt.
b) Bestimme anschließend rechnerisch den Punkt Q(...|6), an dem der Wagen in die Strohballen fährt.
c) Bestimme schließlich die Länge der Strecke, die der Wagen vom Abkommen von der Ideallinie bis zum Aufprall in den Strohballen zurücklegt.