Aufgabe:
Hallo
wir haben die Ableitung einer Funktion gebildet ( Siehe Skript ), die eine Matrix enthält.
Problem/Ansatz:
Problem ist, wohin das \( \vec{h} \) ist. Kann man das etwa einfach weglassen?
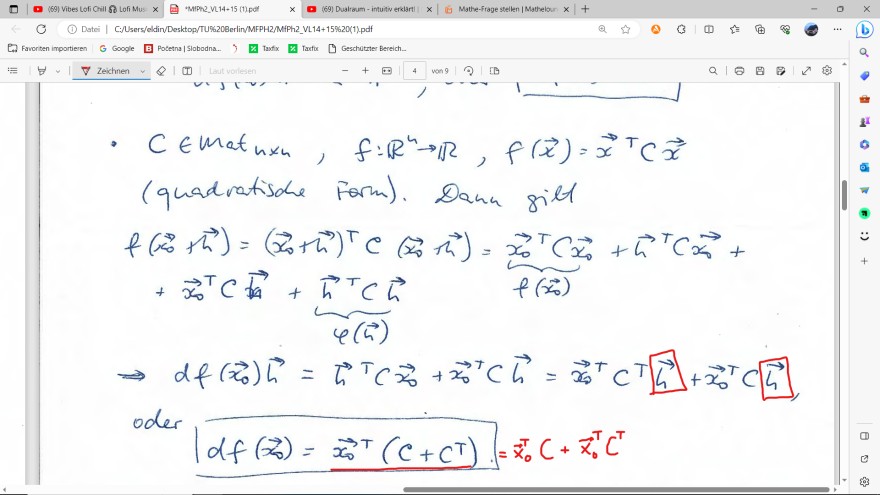
Besagte Stelle ist rot markiert...
Text erkannt:
- \( C \in \) matnxn, \( _{n} \quad f: \mathbb{R}^{n} \rightarrow \mathbb{R}, f(\vec{x})=\vec{x}^{\top} C \vec{x} \) (quadratische Form). Dann gill
\( \begin{array}{l} f\left(\vec{x}_{0}+\vec{h}\right)=\left(\vec{x}_{0}+\vec{h}\right)^{\top} C\left(\vec{x}_{0} \vec{h}\right)=\underbrace{\vec{x}_{0}^{\top} C \vec{x}_{0}}_{f\left(\vec{x}_{0}\right)}+\vec{h}^{\top} C \vec{x}_{0}+ \\ \quad+\vec{x}^{\top} C \overrightarrow{x_{0}}+\underbrace{\vec{h}^{\top} C \vec{h}}_{\varphi(\vec{h})} \\ \Rightarrow \operatorname{df}\left(\vec{x}_{0}\right) \vec{h}=\vec{h}^{\top} C \vec{x}_{0}+\vec{x}_{0}^{\top} C \vec{h}=\vec{x}_{0}^{\top} C^{\top}[\vec{h}]+\vec{x}^{\top} C[\vec{h}], \end{array} \)
oder
\( d f\left(\vec{x}_{0}\right)=\vec{x}_{0}^{\top}\left(C+C^{\top}\right)=\vec{x}_{0}^{T} C+\vec{x}_{0}^{\top} C^{\top} \)
Lg