Aufgabe:
Text erkannt:
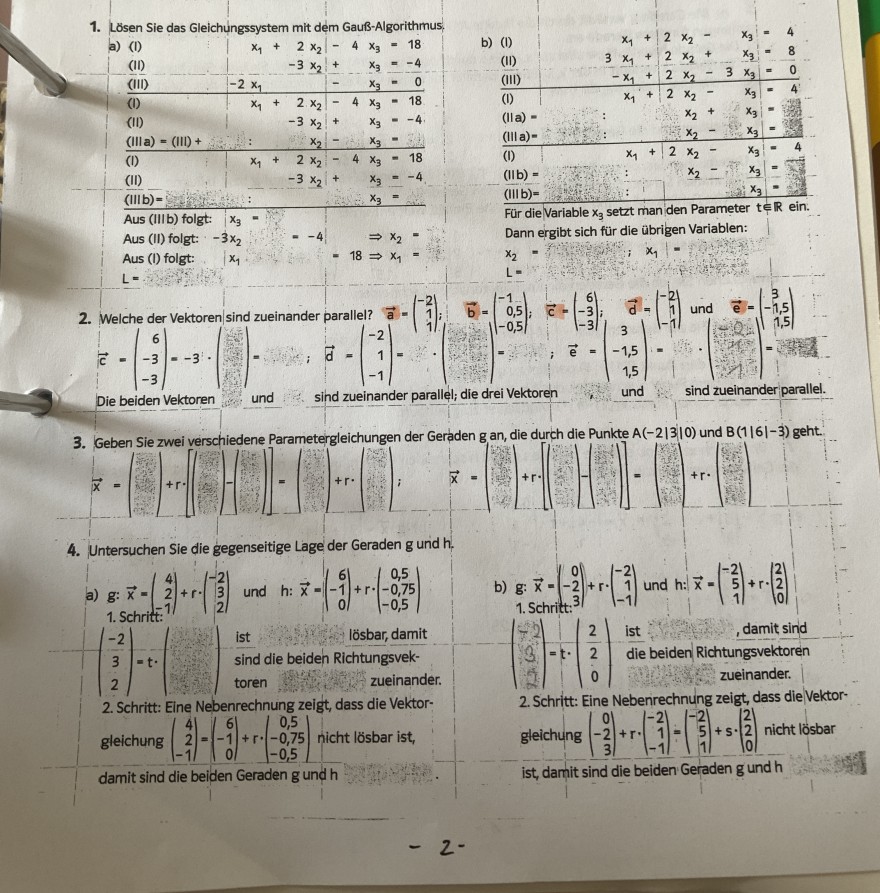
1. Lösen Sie das Gleichüngssystem mit dem Gauß-Algorithmus,
a) (I)
b) (I)
\( x_{1}+2 x_{2}-4 x_{3}=18 \)
(II)
\( x_{1}+2 x_{2}-x_{3} \mid=4 \)
(II)
\( -3 x_{2}+x_{3}=-4 \)
\begin{tabular}{l|r|r} (III) & \( -2 x_{1} \) & \( x_{3}=0 \) \\ \hline (I) & \( x_{1}+2 x_{2}-4 x_{3}=18 \) \\ (II) & \( -3 x_{2}+x_{3}=-4 \) \end{tabular}
\begin{tabular}{l|r|}
(III a) \( = \) (III) + & \( x_{2}-x_{3}= \) \\
\hline (I) & \( x_{1}+2 x_{2}-4 x_{3}=18 \) \\
(II) & \( -3 x_{2}+x_{3}=-4 \)
\end{tabular}
(IIa) \( = \)
\( x_{2}+x_{3}=x_{3} \)
(III a) \( = \) (I)
(IIb) \( = \)
\( x_{2}-\frac{x_{3}}{x_{3}}=x \)
\begin{tabular}{lr} (IIIb) = & \( x_{3}= \) \\ \hline Aus (III) folgt: \( \mid x_{3}= \) & \( \Rightarrow x_{2}= \) \\ Aus (II) folgt: \( -3 x_{2}=-4 \mid \) & \( =18 \Rightarrow x_{1}= \) \\ Aus (I) folgt: \( \mid x_{1} \) & \end{tabular}
(III b) \( = \) Dann ergibt sich für die übrigen Variablen:
\( L= \) \( x_{2}=\quad ; \quad x_{1}= \)
\( L= \)
2. Welche der Vektoren sind zueinander parallel? \( \vec{a}=\left(\begin{array}{r}-2 \\ 1 \\ 1\end{array}\right) \);
\( \vec{b}=\left|\begin{array}{r}-1 \\ 0,5 \\ -0,5\end{array}\right| \)
Die beiden Vektoren und sind zueinander parallel; die drei Vektoren und sind zueinander parallel.
3. Geben Sie zwei verschiedene Parametergleichungen der Geraden g an, die durch die Punkte \( A(-2|3| 0) \) und \( B(1|6|-3) \) geht.
a) \( \mathrm{g}: \overrightarrow{\mathrm{x}}=\left(\begin{array}{r}4 \\ 2 \\ -1\end{array}\right)+r \cdot\left(\begin{array}{r}-2 \\ 3 \\ 2\end{array}\right) \) und \( \mathrm{h}: \overrightarrow{\mathrm{x}}=\left(\begin{array}{c}6 \\ -1 \\ 0\end{array}\right)+r \cdot\left(\begin{array}{c}0,5 \\ -0,75 \\ -0,5\end{array}\right) \)
b) \( g: \vec{x}=\left(\begin{array}{r}0 \\ -2 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{r}-2 \\ 1 \\ -1\end{array}\right) \) und \( h: \vec{x}=\left(\begin{array}{r}-2 \\ 5 \\ 1\end{array}\right)+r \cdot\left(\begin{array}{l}2 \\ 2 \\ 0\end{array}\right) \)
\( \left(\begin{array}{c}-2 \\ 3 \\ 2\end{array}\right)=\mathrm{t} \cdot\left(\begin{array}{l}\text { ist } \\ \text { sind die beiden Richtungsvek- } \\ \text { toren }\end{array}\right. \)
\( \left(\begin{array}{c}-2 \\ 3 \\ 0\end{array}\right)=t \cdot\left(\begin{array}{c}\frac{2}{2} \\ 0\end{array}\right) \)
ist
, damit sind
die beiden Richtungsvektoren
2. Schritt: Eine Nebenrechnung zeigt, dass die Vektor-
2. Schritt: Eine Nebenrechnung zeigt, dass die Vektorgleichung \( \left(\begin{array}{r}4 \\ 2 \\ -1\end{array}\right)=\left(\begin{array}{r}6 \\ -1 \\ 0\end{array}\right)+r \cdot\left(\begin{array}{c}0,5 \\ -0,75 \\ -0,5\end{array}\right) \) nicht lösbar ist, gleichung \( \left(\begin{array}{r}0 \\ -2 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{r}-2 \\ 1 \\ -1\end{array}\right)=\left(\begin{array}{r}-2 \\ 5 \\ 1\end{array}\right)+s \cdot\left(\begin{array}{l}2 \\ 2 \\ 0\end{array}\right) \) nicht lösbar damit sind die beiden Geraden \( \mathrm{g} \) und \( \mathrm{h} \) ist, damit sind die beiden Geraden \( \mathrm{g} \) und \( \mathrm{h} \)
\( -2- \)
Text erkannt:
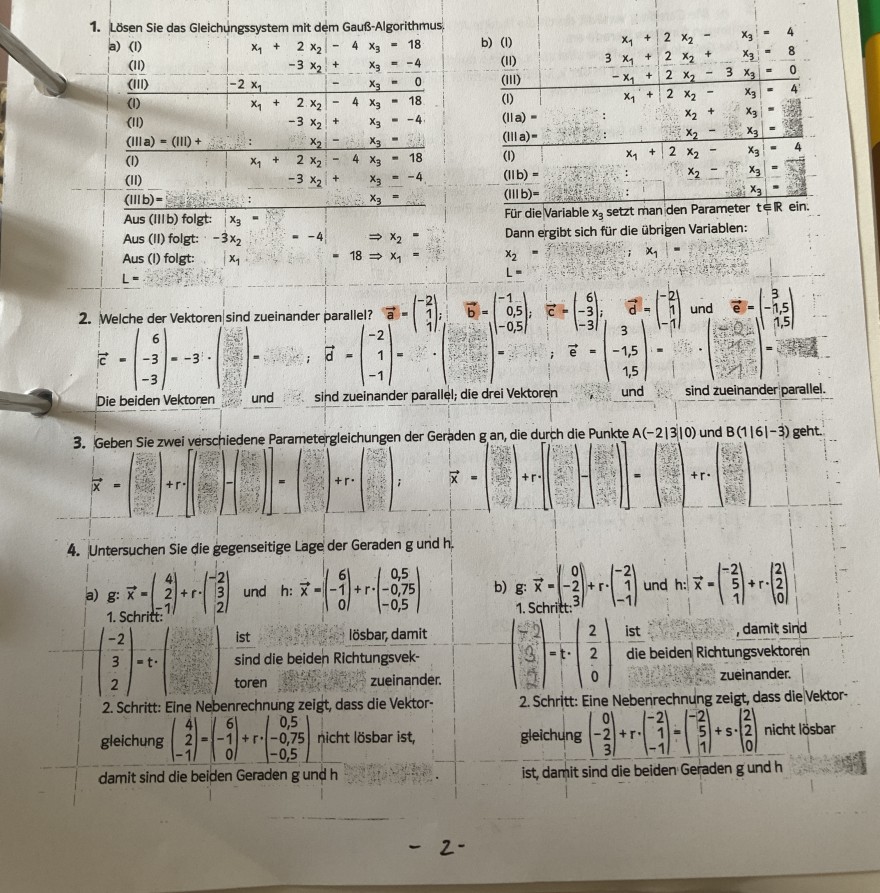
1. Lösen Sie das Gleichüngssystem mit dem Gauß-Algorithmus,
a) (I)
b) (I)
\( x_{1}+2 x_{2}-4 x_{3}=18 \)
(II)
\( x_{1}+2 x_{2}-x_{3} \mid=4 \)
(II)
\( -3 x_{2}+x_{3}=-4 \)
\begin{tabular}{l|r|r} (III) & \( -2 x_{1} \) & \( x_{3}=0 \) \\ \hline (I) & \( x_{1}+2 x_{2}-4 x_{3}=18 \) \\ (II) & \( -3 x_{2}+x_{3}=-4 \) \end{tabular}
\begin{tabular}{l|r|}
(III a) \( = \) (III) + & \( x_{2}-x_{3}= \) \\
\hline (I) & \( x_{1}+2 x_{2}-4 x_{3}=18 \) \\
(II) & \( -3 x_{2}+x_{3}=-4 \)
\end{tabular}
(IIa) \( = \)
\( x_{2}+x_{3}=x_{3} \)
(III a) \( = \) (I)
(IIb) \( = \)
\( x_{2}-\frac{x_{3}}{x_{3}}=x \)
\begin{tabular}{lr} (IIIb) = & \( x_{3}= \) \\ \hline Aus (III) folgt: \( \mid x_{3}= \) & \( \Rightarrow x_{2}= \) \\ Aus (II) folgt: \( -3 x_{2}=-4 \mid \) & \( =18 \Rightarrow x_{1}= \) \\ Aus (I) folgt: \( \mid x_{1} \) & \end{tabular}
(III b) \( = \) Dann ergibt sich für die übrigen Variablen:
\( L= \) \( x_{2}=\quad ; \quad x_{1}= \)
\( L= \)
2. Welche der Vektoren sind zueinander parallel? \( \vec{a}=\left(\begin{array}{r}-2 \\ 1 \\ 1\end{array}\right) \);
\( \vec{b}=\left|\begin{array}{r}-1 \\ 0,5 \\ -0,5\end{array}\right| \)
Die beiden Vektoren und sind zueinander parallel; die drei Vektoren und sind zueinander parallel.
3. Geben Sie zwei verschiedene Parametergleichungen der Geraden g an, die durch die Punkte \( A(-2|3| 0) \) und \( B(1|6|-3) \) geht.
a) \( \mathrm{g}: \overrightarrow{\mathrm{x}}=\left(\begin{array}{r}4 \\ 2 \\ -1\end{array}\right)+r \cdot\left(\begin{array}{r}-2 \\ 3 \\ 2\end{array}\right) \) und \( \mathrm{h}: \overrightarrow{\mathrm{x}}=\left(\begin{array}{c}6 \\ -1 \\ 0\end{array}\right)+r \cdot\left(\begin{array}{c}0,5 \\ -0,75 \\ -0,5\end{array}\right) \)
b) \( g: \vec{x}=\left(\begin{array}{r}0 \\ -2 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{r}-2 \\ 1 \\ -1\end{array}\right) \) und \( h: \vec{x}=\left(\begin{array}{r}-2 \\ 5 \\ 1\end{array}\right)+r \cdot\left(\begin{array}{l}2 \\ 2 \\ 0\end{array}\right) \)
\( \left(\begin{array}{c}-2 \\ 3 \\ 2\end{array}\right)=\mathrm{t} \cdot\left(\begin{array}{l}\text { ist } \\ \text { sind die beiden Richtungsvek- } \\ \text { toren }\end{array}\right. \)
\( \left(\begin{array}{c}-2 \\ 3 \\ 0\end{array}\right)=t \cdot\left(\begin{array}{c}\frac{2}{2} \\ 0\end{array}\right) \)
ist
, damit sind
die beiden Richtungsvektoren
2. Schritt: Eine Nebenrechnung zeigt, dass die Vektor-
2. Schritt: Eine Nebenrechnung zeigt, dass die Vektorgleichung \( \left(\begin{array}{r}4 \\ 2 \\ -1\end{array}\right)=\left(\begin{array}{r}6 \\ -1 \\ 0\end{array}\right)+r \cdot\left(\begin{array}{c}0,5 \\ -0,75 \\ -0,5\end{array}\right) \) nicht lösbar ist, gleichung \( \left(\begin{array}{r}0 \\ -2 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{r}-2 \\ 1 \\ -1\end{array}\right)=\left(\begin{array}{r}-2 \\ 5 \\ 1\end{array}\right)+s \cdot\left(\begin{array}{l}2 \\ 2 \\ 0\end{array}\right) \) nicht lösbar damit sind die beiden Geraden \( \mathrm{g} \) und \( \mathrm{h} \) ist, damit sind die beiden Geraden \( \mathrm{g} \) und \( \mathrm{h} \)
\( -2- \)