Hallo,
John hat einen Handyvertrag.
Wenn er 10 Minuten im Monat telefoniert, so muss er \( 10,90 € \) bezahlen, bei 30 Minuten zahlt er \( 14,30 € \).
Du suchst eine lineare Gleichung der Form y = mx + b mit m = Steigung und b = Schnittpunkt mit der y-Achse.
Du hast die beiden Punkte (10|10,90) und (30|14,30).
m bestimmst du mit den Koordinaten der beiden Punkte in der Formel \(m=\frac{y_1-y_2}{x_1-x_2}\).
[spoiler]
\(m=\frac{10,9-14,3}{10-30}=0,17\)
[/spoiler]
b bestimmt du, indem du die Koordinaten von einem der beiden Punkte und dein Ergebnis für m in die Geradengleichung einsetzt und nach b auflöst.
[spoiler]
\(10,9=0,17\cdot 10+b\\ b=9,2\)
Die Gleichung der Geraden lautet also y = 0,17x + 9,2
[/spoiler]
a) Bestimmen Sie die Funktionsgleichung. ( \( x= \) Minuten, \( y= \) Kosten)
Das solltest du geschafft haben.
b) Wie hoch ist die Grundgebühr und der Preis pro Minute?
m entspricht dem Preis pro Minute, b der Grundgebühr
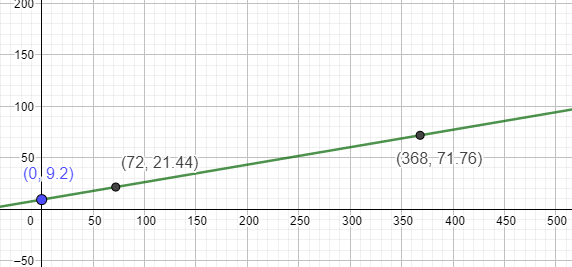
c) Wie viele Minuten hat er telefoniert, wenn er \( 71,76 € \) zahlt?
Setze 71,76 für y ein und löse nach x auf.
d) Wie viel muss er zahlen, wenn er 72 Minuten im Monat telefoniert hat?
Setze 74 für x ein und löse nach y auf.
Melde dich, falls du noch Fragen hast.
Gruß, Silvia