Aufgabe:
Hallo
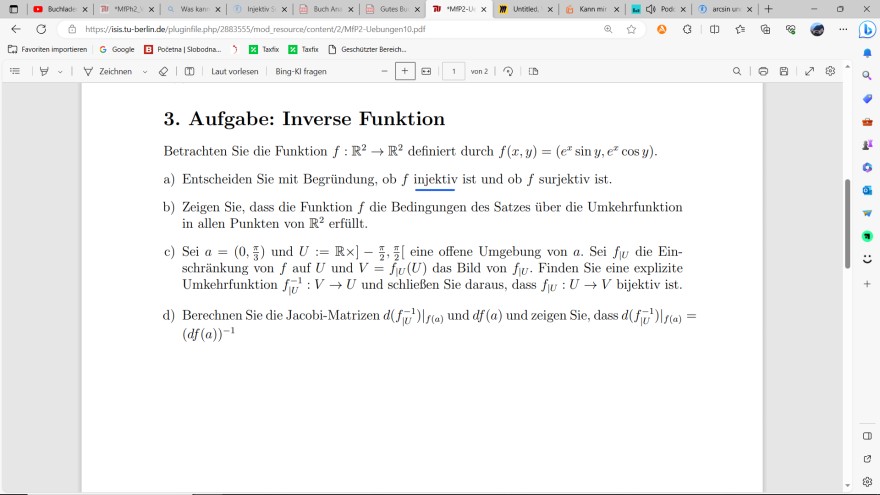
da noch Unsicherheit bzgl Injektivität etc besteht, wäre es cool wenn jemand dies "korrekturlesen" könnte. ( Siehe Bild )
Es geht um 3a)
Text erkannt:
Buchlade
\( x \mid \) तो "Miph 2
Q. Was kan
Injektiv
Buch An
Untitled
Kannmir \( x \mid \) an Clo Pod \( x \mid(1) \) arcsinun \( x \mid+ \) (ब).
Favoriten importieren
G Google
Potetna | Slobodna.
\% Taxtix
X. Tarfie
Geschatrier Bereich.
㫜
Laut vorlesen | Bing-KI fragen
[D
3. Aufgabe: Inverse Funktion
Betrachten Sie die Funktion \( f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2} \) definiert durch \( f(x, y)=\left(e^{x} \sin y, e^{x} \cos y\right) \).
a) Entscheiden Sie mit Begründung, ob \( f \) injektiv ist und ob \( f \) surjektiv ist.
b) Zeigen Sie, dass die Funktion \( f \) die Bedingungen des Satzes über die Umkehrfunktion in allen Punkten von \( \mathbb{R}^{2} \) erfüllt.
c) Sei \( a=\left(0, \frac{\pi}{3}\right) \) und \( \left.U:=\mathbb{R} \times\right]-\frac{\pi}{2}, \frac{\pi}{2}\left[\right. \) eine offene Umgebung von \( a \). Sei \( f_{\mid U} \) die Einschränkung von \( f \) auf \( U \) und \( V=f_{\mid U}(U) \) das Bild von \( f_{\mid U} \). Finden Sie eine explizite Umkehrfunktion \( f_{\mid U}^{-1}: V \rightarrow U \) und schließen Sie daraus, dass \( f_{\mid U}: U \rightarrow V \) bijektiv ist.
d) Berechnen Sie die Jacobi-Matrizen \( \left.d\left(f_{\mid U}^{-1}\right)\right|_{f(a)} \) und \( d f(a) \) und zeigen Sie, dass \( \left.d\left(f_{\mid U}^{-1}\right)\right|_{f(a)}= \) \( (d f(a))^{-1} \)

Text erkannt:
\( H A \wedge O \)
3. \( f_{1} \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}, f(x, y)=\left(e^{x} \sin y, e^{x} \cos y\right) \)
Imj: \( f\left(x_{1}, y_{0}\right)=f\left(x_{2}, y_{2}\right) \stackrel{\operatorname{lol} \operatorname{lo} A}{=}\left(x_{1}, y_{1}\right)=\left(x_{2}, y_{2}\right) \) Bei vehtortunkionen LoS
\( \begin{array}{l} \text { I } e^{x_{1}} \sin y_{1}=e^{x_{2}} \sin y_{2} \\ \text { II } e^{x_{1}} \cos y_{1}=e^{x_{2}} \cos y_{2} \end{array} \)
\( \stackrel{\text { ln }}{\Rightarrow} \)
\( \begin{array}{l} \begin{array}{l} \left.I x_{1}+\ln \left(\sin y_{1}\right)=x_{2}+\ln \left(\sin y_{2}\right)\right]- \\ \text { II } x_{1}+\ln \cos y_{1}=x_{2}+\ln \left(\cos y_{2}\right) \\ \ln \left(\sin y_{1}\right)-\ln \left(\cos y_{1}\right)=\ln \sin y_{2}-\ln \cos y_{2} \mid e^{(-)} \end{array} \\ \cdot \frac{\operatorname{son} y^{1}}{\cos y_{1}}=\frac{\sin y_{2}}{\cos y_{2}} \\ \tan y_{1}=\tan y_{2} \\ y_{1}=y_{2} \text { Einsetsen in I } \\ \Rightarrow \quad e^{x_{1}}=e^{x_{2}}=1 x_{1}=x_{2} \\ \end{array} \)
\( \Rightarrow \) finjebtier
surj.
Bsp: \( \forall y \in Y \quad \exists \) xt \( X: f(x)=y \)
Bei Vektorfunktionen LGS und Variablen unabhängig voneinander umformen \( \rightarrow \) Die Argumente in Fkt-Werten angeben mûssen paarweise gleich sein!
\( f_{1} \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}, f(x, y)=\left(e^{x} \sin y, e^{x} \cos y\right) \)
IU \( =e^{x} \sin y \quad \mid \ln \quad \Rightarrow \ln u=x+\ln \sin y=\frac{x=\ln \sin y-\ln u}{\text { Einsetsin in } \underline{I}} \) II \( v=e^{x} \cos y \)
\( \Rightarrow \text { II } v=e^{\ln \sin y \cdot \ln u}=\frac{\sin y}{u}=>\arcsin v u=y \Rightarrow v \cdot u \leq|n| \Rightarrow v \neq 0 \neq u \)
\( \Rightarrow \) f nievs surpeltsis
Lg