Hallo Anna,
das Entscheidende beim Würfel ist ja, dass er achsenparallel im Koordinatensystem liegt. 'achsenparallel' bedeutet, dass jede Kante des Würfels parallel zu einer der Achsen des Koordinatensystens verläuft. Wenn man also von einer Ecke des Würfels zu einer anderen benachbarten Ecke navigiert, so ändert sich immer genau eine der Koordinaten.
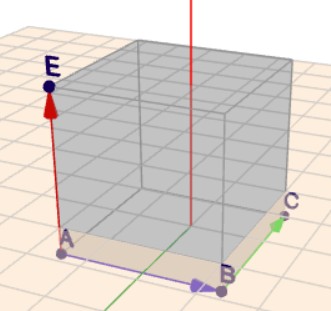
Der Punkt \(A\) liegt bei \(A=(1|\,-2|\,-0,5)\). Der Punkt \(B\) liegt rechts davon - also in positiver Y-Richtung (bzw. \(x_2\)-Richtung). D.h. um von \(A\) nach \(B\) zu kommen, muss die Y-Koordinate (die 2.Koordinate) um die Kantenlänge des Würfels erhöht werden. Die Kantenlänge ist hier 3 (warum?):$$B =A + \begin{pmatrix} 0\\ 3\\ 0 \end{pmatrix} = \begin{pmatrix} 1\\ 1\\ -0,5 \end{pmatrix}$$Dieser Schritt entspricht dem blaue Pfeil im Bild. Dann geht's weiter zu \(C\) in negativer X-Richtung - also muss die X-Koordinate um die Kantenlänge verringert werden (entspricht dem grünen Pfeil). Zu \(D\) geht es weiter, indem man die Y-Koordinate wieder verringert - weil in negative Y-Richtung.
Von \(A\) nach \(E\) komt man durch Erhöhung der Z-Koordinate (der rote Pfeil) und von dort über \(F\) und \(G\) zu \(H\) geht es genau wie unten. \(EFGH\) unterscheidet sich von \(ABCD\) nur durch die Z-Koordinate.
Bei der Pyramide ist es etwas aufwendiger.
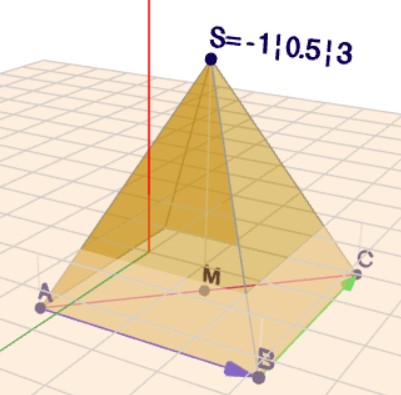
Die Punkte der Grundfläche \(ABCD\) bekommt man hier genau wie beim Würfel. Auch hier sind die Kanten achsenparallel. Dann bestimme den Mittelpunkt \(M\) der Strecke \(AC\), der gleichzeitig der Mittelpunkt der quadratischen Grundfläche ist. Und von \(M\) misst Du in der Zeichnung die Entfernung bis zur Spitze \(S\) (4 LE). Und dies zählst Du zu der Z-Koordinate von \(M\) hinzu, so kommst Du zu \(S\).
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner
