OK, ich nehme Aufgabe c). Wenn du einen Schritt nicht verstehst, sage es!
\(5y=\blue x+25\quad \blue x=2y-7\)
In beiden Gleichungen ist das x enthalten. Bei der 2. Gleichung steht schon x =... Die brauchst du nicht mehr zu verändern.
Die 1. Gleichung formst du entsprechend um:
\(5y=\blue x+25\quad |-25\\ 5y-25=\blue x\)
Bei der 1. Gleichung steht, dass x das Gleiche ist wie 5y - 25 ist.
Bei der 2. Gleichung steht, dass x das Gleiche ist wie 2y - 7
Also kannst du diese beiden Terme gleichsetzen:
\(5y-25=2y-7\quad |-2y\\ 3y-25=-7\quad |+25\\ 3y=18\\ y = 6\)
Damit hast du die y-Koordinate des Schnittpunktes. Um die x-Koordinate zu bestimmen, setzt du dein Ergebnis für y in eine der beiden Gleichungen ein.
Bei der zweiten wäre das:
\( x=2\cdot 6-7=5\)
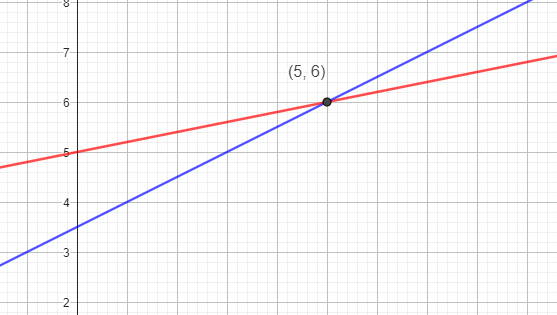
Damit ist der Schnittpunkt