Hallo,
es gibt eine ganze Menge von Verfahren um eine Fläche unter einer Kurve im Allgemeinen und einer Fläche unter einer Parabel im Besonderen näherungsweise zu berechnen.
Eine Möglichkeit für Parabeln - die Du wahrscheinlich nicht in der Schule lernst - ist diese:
Zunächst kannst Du die Fläche abschätzen, indem man einfach das größtmögliche Dreieck abschneidet:
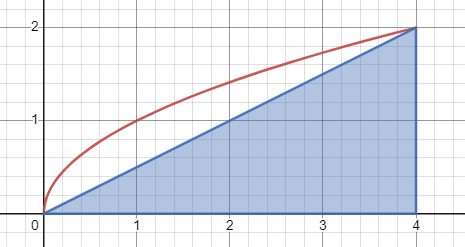
Die blaue Fläche hat den Flächeninhalt \(4\). Das kannst Du selber ausrechnen. Das ist zwar nicht besonders genau, aber es ist eine Größenordnung in der sich die gesuchte Fläche bewegt.
Im nächsten Schritt sucht man sich wieder ein Dreieck aus, was einen möglichst großen Teil der verbleibenden Fläche abdeckt:
.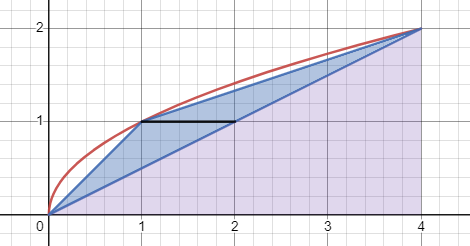
Das ist diesmal das wieder blau markierte Dreieck. Die Fläche lässt sich leicht berechnen, wenn man es durch die schwarze Strecke in zwei Dreiecke unterteilt. Es entstehen zwei Dreiecke mit einer gemeinsamen Grundseite (schwarz) und der gleichen Höhe \(h_1=1\).
Die gleiche Höhe deshalb, weil ich die schwarze Strecke genau auf halber Höhe zwischen \(0\) und \(2\) plaziert habe. Die Koordinaten der schwarzen Strecke sind leicht zu berechnen. Es sind die Punkte \((1;\,1)\) und \((2;\,1)\). D.h. die Länge \(g\) der Strecke ist \(g_1=1\) und wenn ein Dreieck die Fläche \(A_1\) hat, so haben beide zusammen die Fläche:$$\sum A_1 = 2A_1 = 2\left(\frac{h_1 \cdot g_1}{2} \right) = 1$$Damit hat das inzwischen lila und blau markierte Viereck die Fläche \(4+1=5\).
So macht man weiter und fügt weitere Punkte für Dreiecke jeweils auf der Hälfte der senkrechten Abschnitte ein:
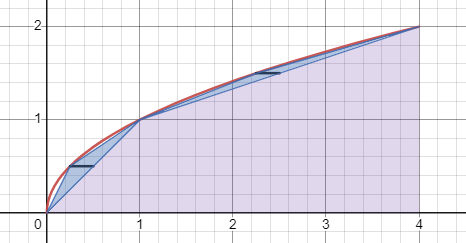
Ich habe die schwarzen Strecken, die zur Berechnung der Flächen dienen, gleich eingezeichnet. Aber bevor ich diese konkret berechne, verallgemeinere ich das auf einen beliebigen Abschnitt auf der Parabel.
Ich betrachte eines der Dreiecke im Intervall \(x \in[a^2;\,b^2]\). Da die Funktion \(f(x)=\sqrt{x}\) lautet, sind die Abschnitte auf der Y-Achse \(a\) und \(b\). Die Y-Koordinate der schwarzen Strecke \(g_k\) liegt in der Mitte zwischen \(a\) und \(b\) also bei \((a+b)/2\).
Die X-Koordinate des linken Endpunktes liegt auf dem Graphen und muss wegen \(f(x)^2=x\) das Quadrat dieses Wertes sein - also \((a+b)^2/4\). Und die X-Koordinate des rechten Endpunkts liegt in der Mitte zwischen \(a^2\) und \(b^2\) ist also \((a^2+b^2)/2\). Folglich ist die Länge \(g_k\) der schwarzen Strecke$$g_k= \frac{a^2+b^2}{2} - \frac{(a+b)^2}{4} = \frac{(a-b)^2}{4}$$Und die Höhe \(h_k\) der beiden Teildreiecke ist \(h_k=(b-a)/2\). Folglich ist die Gesamtfläche im \(k\)'ten Schritt$$\sum A_k = 2\left(\frac{h_k \cdot g_k}{2}\right)= 2\left(\frac{\frac{b-a}{2} \cdot \frac{(a-b)^2}{4}}{2}\right) = \frac{(b-a)^3}{8}$$Damit hängt die Größe der neu hinzu gekommenen Dreicke nur von der Differenz \((b-a)\) auf der Y-Achse ab. Im dritten Bild von oben war diese Differenz \(=1\), folglich hat eines der Dreiecke die Fläche \(1/8\) und da es zwei sind, ist die hinzu gekommende Fläche \(=1/4\). Die neue Gesamtfläche ist \(4+1+1/4 = 5,25\).
Da die Differenz \((b-a)\) sich mit jedem Schritt halbiert, verkleinert sich \(A_k\) wegen der 3.Potenz auf \(1/8\) \(\implies A_{k+1} = A_k/8\). Aber da sich die Anzahl der neu hinzu gekommenden Dreiecke verdoppelt, ist die neue Fläche ein Viertel der vorhergenden. Mit weiteren zwei Schritten ist man dann bei$$F\approx 4 +1 + \frac{1}{4} +\frac{1}{16} + \frac{1}{64} {\color{grey}+ \dots} \\ \phantom{F} = 5 + \frac{16+4+1}{64} \\ \phantom{F} = 5+\frac{21}{64} \approx 5,33$$Das ist bereits eine ziemlich gute Näherung für die Fläche unter der Kurve \(f(x)=\sqrt{x}\) zwischen \(x=0\) und \(x=4\).
Gruß Werner
PS.: habt Ihr geometrische Reihen schon durch genommen?