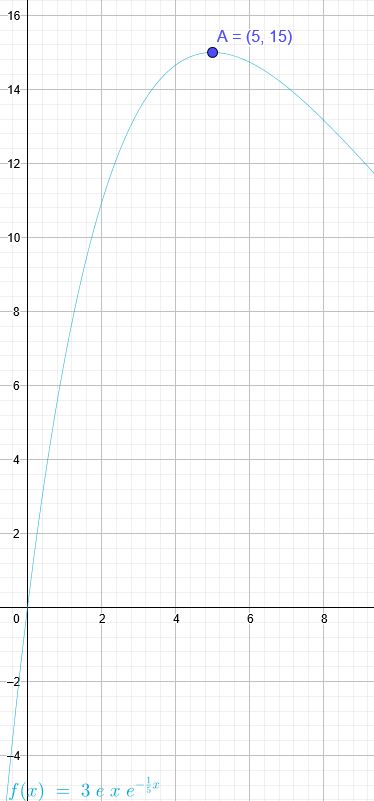
Die Konzentration eines Medikaments im Blut kann durch eine Funktion der Form \(f(t)= a*t*e^{-b*t}+c\) beschrieben werden. Dabei wird t in Stunden nach der Einnahme gemessen, die Konzentration in mg/l.
Bei einem Versuch wird die höchste Konzentration mit 15 mg/l nach 5 Stunden gemessen. Bestimmen sie a und b.
\(f(t)= a*t*e^{-b*t}+c\)
Da die Konzentration des Medikaments im Blut zum Zeitpunkt 0 auch 0 ist gilt \(c=0\)
\(f(t)= a*t*e^{-t*b}\)
\(f(5)= a*5*e^{-5*b}\)
\( a*5*e^{-5*b}=15\)
1.)
\( a*e^{-5*b}=3\)
\(f´(t)= a*e^{-t*b}+a*t*e^{-t*b}*b\)
\(f´(5)= a*e^{-5*b}+a*5*e^{-5*b}*b\)
2.)
\( a*e^{-5*b}+5a*b*e^{-5*b}=0\)
\( 3+15b=0\)
\( b=\frac{1}{5}\)
\( a*e^{-5*\frac{1}{5}}=3\)
\( a*e^{-1}=3\)
\( a=3e\)
\(f(t)= 3e*t*e^{-\frac{1}{5}*t}\)