 Aufgabe:
Aufgabe:
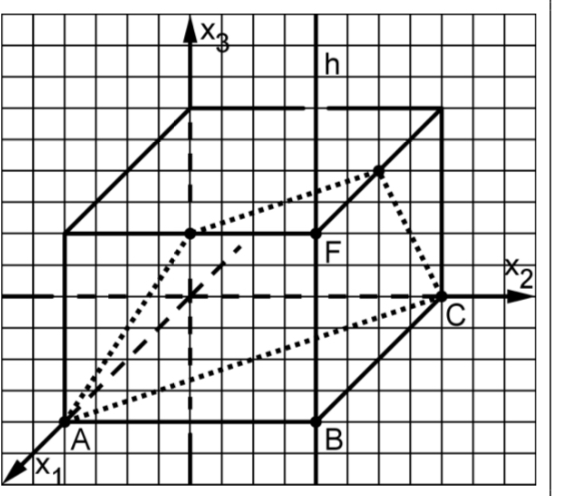
Die Punkte A(4|0|0), B(4|4|0), C(0|4|0) und F(4|4|3) sind Eckpunkte
des abgebildeten Quaders. Die Gerade h verläuft durch B und F.
a Begründen Sie, dass das Dreieck ABC rechtwinklig und gleichschenklig ist. Geben 3 Sie den Flächeninhalt dieses Dreiecks an.
b Geben Sie eine Gleichung der Gerade an, die durch A und C verläuft. Begründen Sie, 3 dass diese Gerade windschief zur Gerade h ist.
Die Abbildung zeigt gepunktet die Seiten der Schnittfigur des Quaders und einer Ebene, in der die Punkte A und C sowie ein Punkt P der Gerade h liegen. Diese Ebene zerlegt den Quader in zwei Teilkörper.
c Beschreiben Sie, wie man mithilfe der Abbildung ermitteln kann, dass P die x3 -Koordinate 6 hat.
d Berechnen Sie das Volumen desjenigen der beiden Teilkörper, zu dem der Punkt B 5 gehört, und erläutern Sie Ihr Vorgehen.
Die Punkte der Gerade h lassen sich durch Pt (4 | 4 | t) mit t ∈IR darstellen. Für jeden WertvontliegenA,CundPt inderEbeneEt:t⋅x1+t⋅x2−4⋅x3−4t=0.DabeiistE6 diejenige Ebene, für die in der Abbildung die Seiten der Schnittfigur dargestellt sind.
e Zeigen Sie, dass der Punkt (0 | 0 | 2) der Schnittpunkt der Ebene E−2 mit der 2 x3 -Achse ist.
f Es gibt Werte von t, für die die Schnittfigur des Quaders und der Ebene Et nicht die 4 Form eines Vierecks, sondern die eines Dreiecks hat. Geben Sie alle diese Werte
von t an und beschreiben Sie in Abhängigkeit von t die Lage der Eckpunkte des Drei- ecks.
Problem/Ansatz:
Ab der Aufgabe c habe ich Schwierigkeiten, ich wüsste nicht wie man dort nur mit der Abbildung hinkommt, mit der Rechnung ja, aber nur mit Beschreiben nein. Ab danach finde ich es irgendwie auch recht schwer ?