Aufgabe:
Ein Sendemast (siehe Abb. 3) mit einer Höhe
von 200 Metern steht an der Stelle F = (010|0)
senkrecht auf den Boden. Der Sendemast wird von der Sonne beschienen und wirft einen Schatten auf dem Boden. Die Sonne strahlt in Richtung des Vektors:
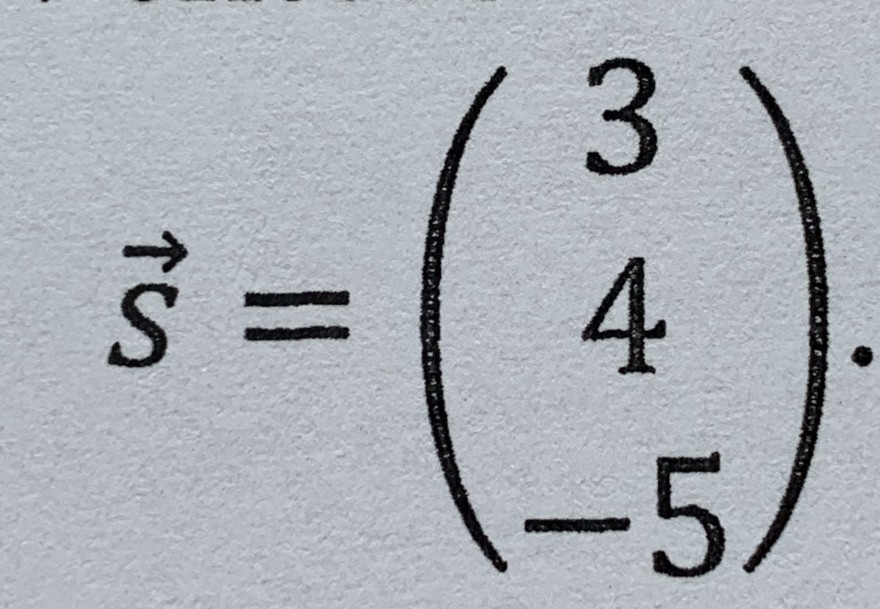
Text erkannt:
\( \vec{s}=\left(\begin{array}{c}3 \\ 4 \\ -5\end{array}\right) \)
Die Werte sind in Metern angegeben.
a) Entwerfen Sie eine Skizze und beschreiben
Abb. 3: Sendemasten in
Moorfleet
Sie wie Sie vorgehen können, um die Länge des Schattens zu berechnen, den der Sendemast wirft.
b) Berechnen Sie die Länge des Schattens, den der Sendemast wirft.
Problem/Ansatz:
Ich komme bei dieser Aufgabe leider überhaupt nicht weiter. Da wir uns aber daran probieren sollen und ich es gerne verstehen wollen würde, würde ich mich sehr über eine Erklärung freuen, wie ich sie lösen kann.