Berechnen sie mithilfe der Schattenpunkte von A und B die Länge des Schattens der Strecke AB.

Question

Aufgabe:

Die Punkte A (1/3/9) und B 1/7/12) sind die Endpunkte der Strecke AB. Im Punkt P (2/4/5) befindet sich eine punktförmige Lichtquelle, die einen Schatten der Strecke AB auf die

Ebene E: x= -2/0/1 + r• 1/1/1 + s• -2/2/1

wirft.

Berechnen sie mithilfe der Schattenpunkte von A und B die Länge des Schattens der Strecke AB.

Problem/Ansatz:

Ich versuche seit einer Stunde, die Aufgabe zu lösen, komme aber mit den bisherigen Erklärungen aus anderen Foren nicht weiter. Wenn es eine x1x2-Ebene wäre, hätte ich glaube ich noch gewusst, was ich tun muss, aber das kann man hier ja nicht ablesen (glaube ich?)

Comments

Anbei mal eine Szene nach der Beschreibung aus Deiner Aufgabe (klick auf das Bild).

Der Punkt \(P\) liegt direkt in \(E\) (\(r=4\) und \(s=0\)) und kann somit schwerlich einen Schatten in \(E\) werfen. Checkst Du bitte nochmal die Angaben aus Deiner Aufgabe

---

Sorry,  der Punkt P lautet (2/4/15)

---

Ok - das sieht gut aus. Kannst Du die Parameterfrom der Ebene in Koordinatenform umwandeln oder rechnet Ihr Schnittpunkte Ebene mit Gerade beides in Parameterform?

---

Wir rechnen alles in Parameterform

Answer 1

Berechne den Schnittpunkt der Gerade PA mit E.

Berechne den Schnittpunkt der Gerade PB mit E.

Answer 2

Hallo,

dann sieht die Szene so aus:

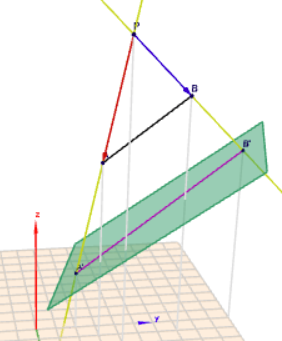
Stelle die beiden Geradengleichungen für die Strahlen durch \(P\) und \(A\) und durch \(P\) und \(B\) auf.$$g_a \quad \vec x = \begin{pmatrix}2\\ 4\\ 15\end{pmatrix} + \begin{pmatrix}-1\\ -1\\ -6\end{pmatrix} t\\ g_b \quad \vec x = \begin{pmatrix}2\\ 4\\ 15\end{pmatrix} + \begin{pmatrix}-1\\ 3\\ -3\end{pmatrix} u$$und berechne die Schnittpunkte dieser Geraden mit der Ebene \(E\).

In Parameterform setze die Ebenengleichung mit einer der gewünschten Geradengleichungen gleich$$E = g_a \implies \\ \begin{pmatrix}-2\\ 0\\ 1\end{pmatrix} + \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}r + \begin{pmatrix}-2\\ 2\\ 1\end{pmatrix}s = \begin{pmatrix}2\\ 4\\ 15\end{pmatrix} + \begin{pmatrix}-1\\ -1\\ -6\end{pmatrix} t$$umsortieren gibt$$\begin{pmatrix}1\\ 1\\ 1\end{pmatrix} r + \begin{pmatrix}-2\\ 2\\ 1\end{pmatrix}s + \begin{pmatrix}1\\ 1\\ 6\end{pmatrix}t = \begin{pmatrix}4\\ 4\\ 14\end{pmatrix} $$Es reicht, das \(t\) zu isolieren. Ziehe dazu die erste Zeile bzw. Gleichung (die X-Koordinate) von den anderen beiden Zeilen ab. ich schreibe nur noch die Koeffizienten:$$\begin{array}{ccc|c}1& -2& 1& 4\\ 0& 4& 0& 0\\ 0& 3& 5& 10\end{array}$$Aus der zweiten Zeile folgt bereits \(s=0\) und wenn man dies in die dritte Zeile einsetzt, so wird \(t=2\). Mit \(t=2\) gehe nun in die Geradengleichung \(g_a\) und Du erhältst den Schnittpunkt \(A'\) von \(g_a\) mit \(E\). Das Verfahren mit \(g_b\) ist natürlich identisch.

Die Schnittpunkte, und damit die Endpunkte des Schattens der Strecke, sind$$A' = \begin{pmatrix}0\\ 2\\ 3\end{pmatrix}, \quad B' = \begin{pmatrix}0\\ 10\\ 9\end{pmatrix}$$und die Länge ist der Betrag der Differenz$$|A'B'| = \left| \begin{pmatrix}0\\ 10\\ 9\end{pmatrix} - \begin{pmatrix}0\\ 2\\ 3\end{pmatrix}\right| = 10$$Falls Du noch Fragen hast, so melde Dich bitte.

Gruß Werner

Comments

Hi :)

Könntest du mir bitte bei meine neusten Frage helfen.

Vor allem, wie man die Stützpunkte einsetzt und in den Integrand einsetzt, da keine Formel gegeben ist(nur Stützpunkte).

Wäre dir sehr dankbar, wenn du mir helfen könntest :)

---

Könntest du vielleicht einmal kurz erklären, wie du die Gleichung mit der Ebene und der abgerissen umsortiert hast? Ich kann das nicht so ganz nachvollziehen

---

Könntest du vielleicht einmal kurz erklären, wie du die Gleichung mit der Ebene und der abgerissen umsortiert hast?

Meinst Du dies?$$E = g_a \implies \\ \begin{aligned}\begin{pmatrix}-2\\ 0\\ 1\end{pmatrix} + \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}r + \begin{pmatrix}-2\\ 2\\ 1\end{pmatrix}s &= \begin{pmatrix}2\\ 4\\ 15\end{pmatrix} + \begin{pmatrix}-1\\ -1\\ -6\end{pmatrix} t &&\left|\,- \begin{pmatrix}-1\\ -1\\ -6\end{pmatrix} t \right. \\ \begin{pmatrix}-2\\ 0\\ 1\end{pmatrix} + \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}r + \begin{pmatrix}-2\\ 2\\ 1\end{pmatrix}s + \begin{pmatrix}1\\ 1\\ 6\end{pmatrix} t &= \begin{pmatrix}2\\ 4\\ 15\end{pmatrix} &&\left|\,- \begin{pmatrix}-2\\ 0\\ 1\end{pmatrix} \right.\\ \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}r + \begin{pmatrix}-2\\ 2\\ 1\end{pmatrix}s + \begin{pmatrix}1\\ 1\\ 6\end{pmatrix} t &= \begin{pmatrix}2\\ 4\\ 15\end{pmatrix}- \begin{pmatrix}-2\\ 0\\ 1\end{pmatrix} \\ \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}r + \begin{pmatrix}-2\\ 2\\ 1\end{pmatrix}s + \begin{pmatrix}1\\ 1\\ 6\end{pmatrix} t &= \begin{pmatrix}2+2\\ 4-0\\ 15-1\end{pmatrix}\\ \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}r + \begin{pmatrix}-2\\ 2\\ 1\end{pmatrix}s + \begin{pmatrix}1\\ 1\\ 6\end{pmatrix} t &= \begin{pmatrix}4\\ 4\\ 14\end{pmatrix}\end{aligned}$$

---

wieso stehen hier in der Matrix andere Zahlen als in der gleichung?

---

wieso stehen hier in der Matrix andere Zahlen als in der gleichung?

weil die Matrix bereits das Resultat(!) der im Text darüber beschriebenen Rechnung enthält. Wenn ich nur die Koeffizienten schreibe, dann steht da:$$\begin{array}{ccc|c}1& -2& 1& 4\\ 1& 2& 1& 4\\ 1& 1& 6& 14\end{array}$$das ist eine Kopie der Gleichung mit den Vektoren. Ich schrieb dann (s.o.)

Es reicht, das \(t\) zu isolieren. Ziehe dazu die erste Zeile bzw. Gleichung (die X-Koordinate) von den anderen beiden Zeilen ab.

tut man das, was da steht, so wird daraus:$$\begin{array}{ccc|c}1& -2& 1& 4\\ 0& 4& 0& 0\\ 0& 3& 5& 10\end{array}$$