Wird der Parameter σ einer Normalverteilung halbiert, so wird die Glockenkurve schmäler

Question

Aufgabe:

Wird der Parameter σ einer Normalverteilung halbiert, so wird die Glockenkurve schmäler

Problem/Ansatz:

Ich verstehe diesen Satz nicht? Wieso ist das so? Wieso wird sie nicht breiter

Answer 1

Wird die Standardabweichung \(\sigma\) kleiner, sind doch mehr Werte in der Nähe des Mittelwerts \(\mu\), so dass die Glocke schmaler wird.

Answer 2

Aloha :)

Die Gauß'sche Glockenkurve hat 2 Wendepunkte. Der linke Wendepunkt hat den Abstand \((-\sigma)\) vom Nullpunkt und der rechte Wendepunkt hat den Abstand \((+\sigma)\) vom Nullpunkt.

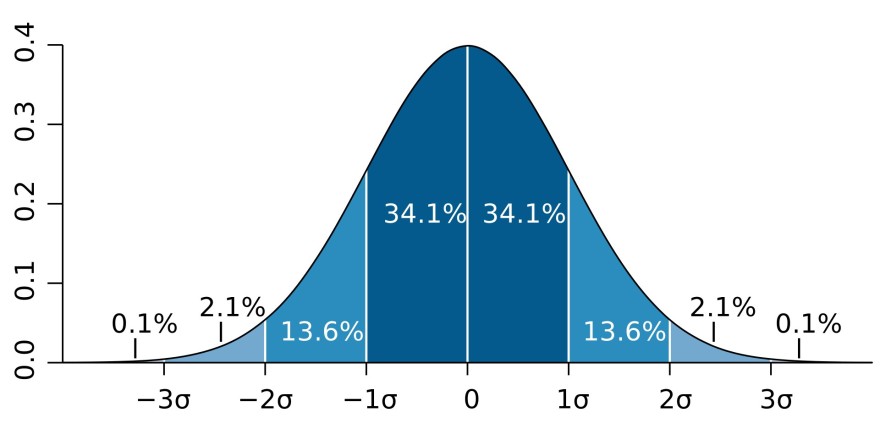
In der Abbildung ist das der dunkelblaue Bereich. Wenn die Standardabweichung \(\sigma\) halbiert wird, rücken die beiden Wendepunkte näher zusammen und der dunkelblaue Bereich wird schmaler.