Aloha :)
In einem rechtwinkligen Dreieck gibt es die Hypotenuse \(c\) (längste Seite), die Ankathete \(b\) (liegt an dem Winkel) und die Gegenkathete \(a\) (liegt dem Winkel gegenüber).
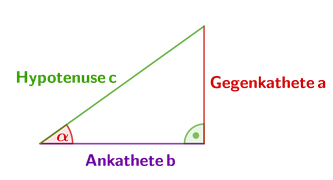
Mit der Cosinus-Funktion wird die Hypotenuse \(c\) auf die Ankathete \(b\) projeziert:$$b=c\cdot\cos(\alpha)$$Mit der Sinus-Funktion wird die Hypthenuse \(c\) auf die Gegenkathete \(a\) projeziert:$$a=c\cdot\sin(\alpha)$$
Zum Merken kannst du dir das \(c\) vom \(\cos\) als Winkel vorstellen$$\pink{\operatorname{c}}\!\operatorname{os}\cos(\alpha)\;\to\;\pink{\angle}\!\operatorname{os}(\alpha)$$
\(\pink{\angle}\) = Die lange Seite wird mit dem Cosinus des Winkels auf die kurze Seite projeziert.
Das funktioniert natürlich auch, wenn das rechtwinklige Dreieck "verdreht" ist:
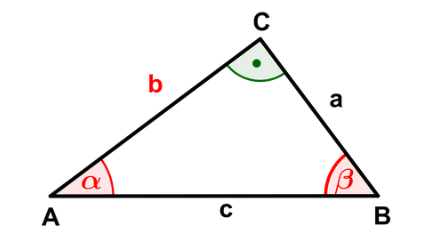
$$b=c\cdot\cos(\alpha)\quad;\quad a=c\cdot\cos(\beta)$$$$b=c\cdot\sin(\beta)\quad;\quad a=c\cdot\sin(\alpha)$$
Offensichtlich ist \(\pink{\cos(\alpha)=\sin(\beta)}\) und \(\pink{\cos(\beta)=\sin(\alpha)}\).
Dieser Eigenschaft verdanken die co-Funktionen ihren Namen. Mit der jeweiligen co-Funktion geht man zum complementären Winkel über, das ist in einem rechtwinkligen Dreieck der andere Nicht-90-Grad-Winkel. Allgemein heißt das:$$\sin(\alpha)=\cos(\beta)=\cos(90^\circ-\alpha)$$$$\cos(\alpha)=\sin(\beta)=\sin(90^\circ-\alpha)$$$$\tan(\alpha)=\cot(\beta)=\cot(90^\circ-\alpha)$$$$\cot(\alpha)=\tan(\beta)=\tan(90^\circ-\alpha)$$
Jetzt sollte dir die geometrsiche Bedeutung der Sinus- und Cosinus-Funktionen ein bisschen klarer geworden sein.