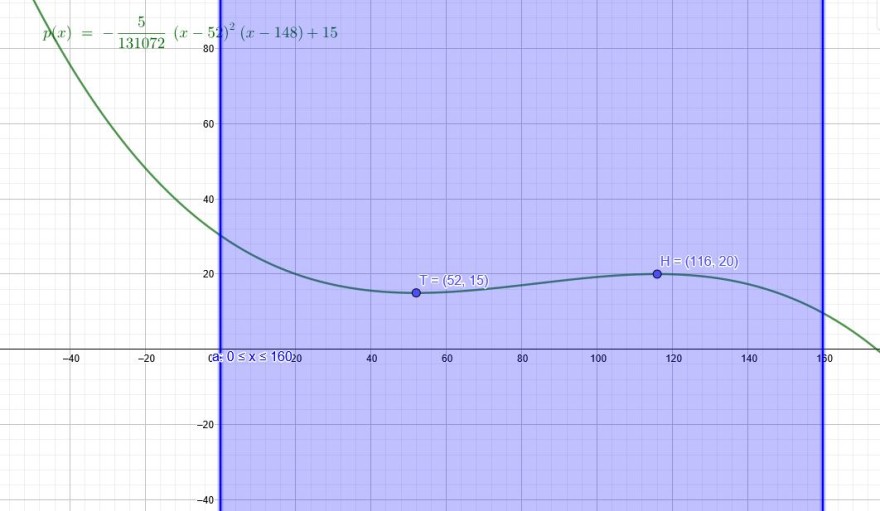
Das Profil einer Gartenliege kann im Intervall [0; 160] durch eine Polynomfunktion
3. Grads beschrieben werden. Die Funktion hat in T(52| 15) einen Tiefpunkt und in
H(116|20) einen Hochpunkt (Angaben in cm).
1) Stelle das Gleichungssystem auf, mit dem man die Koeffizienten der Polynomfunktion bestimmen kann.
2) Löse das Gleichungssystem und gib die Funktionsgleichung an.
3) Stelle das Profil der Liege grafisch dar und bestimme den Neigungswinkel im höchsten
Punkt der Liege.
Ich verschiebe den Graph um 15 Einheiten nach unten:
\(T(52| 15) →T´(52| 0)\) Da ist nun eine doppelte Nullstelle
\(f(x)=a\cdot(x-52)^2 \cdot (x-N)\)
\(H(116|20)\)→\(H´(116|5)\)
\(f(116)=a\cdot(116-52)^2 \cdot (116-N)=4096a \cdot (116-N)\)
1.) \(4096a \cdot (116-N)=5 \)
\(f(x)=a\cdot[(x-52)^2 \cdot (x-N)]\)
\(f´(x)=a\cdot[2\cdot(x-52) \cdot (x-N)+(x-52)^2]\)
\(f´(116)=a\cdot[2\cdot(116-52) \cdot (116-N)+(116-52)^2]=0\)
\(N=148\) ∈ 1.) \(4096a \cdot (116-148)=5 \)
\(a=-\frac{5}{131072}\)
\(f(x)=-\frac{5}{131072}\cdot(x-52)^2 \cdot (x-148)\)
Nun 15 Einheiten nach oben:
\(p(x)=-\frac{5}{131072}\cdot(x-52)^2 \cdot (x-148)+15\)