Fermat-Punkt im Quadrat

Question

Gibt es so etwas wie einen Fermat-Punkt im Quadrat? Also einen Punkt P, sodass die Summe der Abstäne zu den vier Ecken des Quadrats minimal wird. Ich vermute mal, dass solch ein Punkt, wenn es ihn gibt, auf dem Schnittpunkt der Diagonalen liegt. Ich habe aber leider keine Ahnung wie man so etwas beweisen könnte. Würde mich sehr über Hilfe freuen :)

Comments

Hallo,

wenn es nur genau ein Punkt sein soll, so hat abakus dazu schon geantwortet.

Wenn Du aber einen Streckenzug minimaler Länge suchst, der alle vier Eckpunkte mit einander verbindet, so gibt es noch eine weitere (bzw. zwei) Lösung(en), mit einem kürzerem Streckenzug als \(2\sqrt{2}\,a\). (\(a\) sei die Kantenlänge des Quadrats)

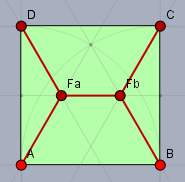
Die Gesamtstrecke ist hier \(\left(1+\sqrt{3}\right)a \approx 2,73a\) gegenüber \(2\sqrt{2}\,a \approx 2,83a\). Für die zweite Lösung dreht man das ganze um 90°.

Bei einem Rechteck liegt die Strecke \(F_aF_b\) parallel zur längeren Seite.

---

Genau, das war eigentlich nicht das, was ich gesucht hatte, aber trotzdem vielen Dank! :)

Answer 1

Deine Vermutung ist richtig. Würde der Punkt P nicht auf der Diagonalen AC liegen. wäre wegen der Dreiecksungleichung die Summe seiner Abstände zu A und zu C größer als diese Diagonalenlänge. Gleiches gilt für die Diagonale BD und die Abstände von P zu B bzw. D.

Comments

Stimmt, vielen Dank! :)