Bestimme eine Funktionsgleichung dieses parabelförmigen Eingangs.

Question

Aufgabe:

Oftmals werden Kellertüren durch Bögen abgestützt, um die Lasten des darüber liegen- den Mauerwerks gut zu verteilen. Das Wein- gut „Riesling“ plant für den Weinkeller den Bau eines neuen parabelförmigen Eingangs. Um mit einem Gabelstapler in den Wein- keller fahren zu können, muss der Eingang nebenstehende Bedingungen erfüllen:
a) Bestimme eine Funktionsgleichung dieses parabelförmigen Eingangs.
b) Wie hoch muss der Keller mindestens sein, damit man den Eingang in dieser Form
mauern kann?

Problem/Ansatz:

Dies ist eine Übung für unsere Arbeit, ich weiß aber nicht, wie ich auf die Lösung kommen kann. Kann mir bitte jemand helfen? Danke schon mal!!

Answer 1

Hallo,

lege die linke untere Ecke des Eingangs in den Koordinatenursprung.

Du kennst jetzt

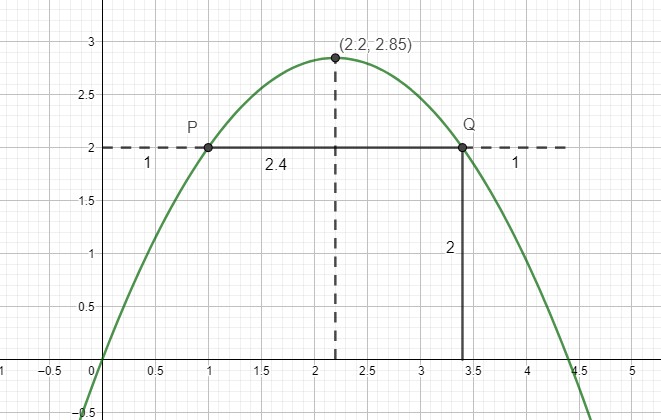
die beiden Nullstellen der Parabel bei x = 0 und x = 4,4

(die x-Koordinate des Scheitelpunktes S = 2,2)

zwei Punkte mit den Koordinaten P (1|2) bzw. Q (3,4|2)

allgemeine Gleichung einer Parabel: \(f(x)=ax^2+bx+c\)

c bezeichnet den Schnittpunkt mit der y-Achse, hier also c = 0

Jetzt brauchst du noch zwei Gleichungen, um die Unbekannten a und b zu bestimmen. Setze dazu die Koordinaten der beiden Punkte in die Gleichung ein.

\(P(1\mid2)\rightarrow a + b = 2\rightarrow a=2-b\\ Q(3,4\mid2)\rightarrow 11,56a+3,4b=2\)

Wende beispielsweise das Einsetzungsverfahren an:

\(11,56(2-b)+3,4b=2\\ b=\frac{44}{17}\\ a=-\frac{10}{17}\)

Die Funktionsgleichung lautet also \(f(x)=-\frac{10}{17}x^2+\frac{44}{17}x\)

Die Mindesthöhe des Kellers entspricht der y-Koordinate des Scheitelpunktes.

Umwandlung von der Normalform in die Scheitelpunktfrom mit Hilfe der quadratischen Ergänzung:

\(f(x)=-\frac{10}{17}x^2+\frac{44}{17}\\ =-\frac{10}{17}(x^2-4,4x)\\ =-\frac{10}{17}((x-2,2)^2-4,84)\\ =-\frac{10}{17}(x-2,2)^2+2,85\)

Der Keller muss also mindestens 2,85 m hoch sein.

Gruß, Silvia

Comments

Vielen Dank, Sie haben mich gerettet!!!!

Answer 2

Man kann es sich auch ganz einfach machen:

Koordinatenursprung in den Scheitelpunkt der Parabel legen und y-Achse nach unten:

\(\Rightarrow f(x) = ax^2\) mit

\(f(1.2) = 1.44a=h-2\quad (1)\)

\(f(2.2) = 4.84 a = h \quad (2)\)

\(\stackrel{(2)-(1)}{\Rightarrow} 3.4a=2 \Rightarrow a= \frac{10}{17}\)

\(\Rightarrow h= 4.84 \cdot \frac{10}{17} \approx 2.85\)

Answer 3

a) f(x) = ax^2+bx+c

f(1) = 2

f(3,4) = 2

f(4,4) = 0

Answer 4

Ich wähle die y-Achse als Symmetrieachse der Parabel:

Berechnung über die Nullstellenform der Parabel:

\(f(x)=a\cdot(x+2,2)\cdot(x-2,2)\)

\(P(1,2|2)\)

\(f(1,2)=a\cdot(1,2+2,2)\cdot(1,2-2,2)=a*3,4\cdot(-1)=-3,4a\)

\(-3,4a=2\) →  \(a=-0,588235\)

\(f(x)=-0,588235\cdot[(x+2,2)\cdot(x-2,2)]=-0,588235\cdot[(x+2,2)\cdot(x-2,2)]\)

Höhe des Kellers:

\(f(0)=-0,588235\cdot[(0+2,2)\cdot(0-2,2)]=-0,588235\cdot(-4,84)]=2,85\)