Hallo,
a) Bestimme eine Funktionsgleichung g der parabelförmigen Brücke, bei der der linke Punkt der Brücke im Koordinatenursprung liegt. Spannweite 60, Höhe 18 m
Du kennst zwei Nullstellen der Parabel bei x = 0 und x = 60 und den Scheitelpunkt (30|18)
Die Gleichung hat also die Form \(f(x)=a(x-30)^2+18\).
a berechnest du, indem du 0 oder 60 für x einsetzt.
[spoiler]
\(f(x)=a(x-30)^2+18\\ 0=900a+18\Rightarrow a=-\frac{1}{50}\)
[/spoiler]
b) Für bessere Stabilität der Brücke wurden 11 senkrechte Träger in gleichen Abständen eingezogen. Berechne die Länge des 2. und 6. Trägers.
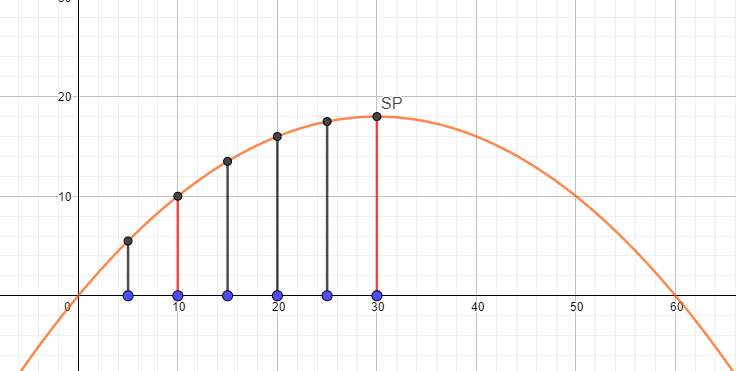
Rechts und links vom Scheitelpunkt werden jeweils noch 5 Träger eingezogen, also bei x = 5, 10, 15, 20, 25, 35, 40, 45, 50 und 55.
Du musst also f(10) und f(30) berechnen.
c) Berechne, wie lang die Brücke wäre, wenn sie nur 15 Meter hoch wäre.
Berechne den Abstand der Nullstellen der Funktion \(f(x)=-\frac{1}{50}(x-30)^2+15\)
Gruß, Silvia