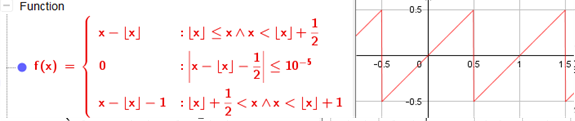Kann ich die Funktion irgendwo zeichnen lassen?

Question

$$ ((x)):=\left\{\begin{array}{ll} x-\lfloor x\rfloor, & \lfloor x\rfloor \leq x<\lfloor x\rfloor+\frac{1}{2} \\ 0, & x=\lfloor x\rfloor+\frac{1}{2} \\ x-\lfloor x\rfloor-1, & \lfloor x\rfloor+\frac{1}{2}<x<\lfloor x\rfloor+1 \end{array} .\right.$$

Problem/Ansatz:

Kann ich die Funktion irgendwo zeichnen lassen? Habe es bei Desmos probiert aber das klappt nicht. Vielleicht mache ich was falsch

Answer 1

zum Beispiel

GeoGebra

und vielleicht besser

g(x) = If(floor(x) ≤ x < floor(x) + 1 / 2, x - floor(x), x == floor(x) + 1 / 2, 0, floor(x) + 1 / 2 < x < floor(x) + 1, x - floor(x) - 1)

Comments

.. und der Rest ist Hausaufgabe

---

... und in Desmos

wenn's nur um das Zeichnen geht, dann wäre das eine Möglichkeit.

---

und jetzt ist es auch eine 'richtige' Funktion in Desmos ;-)

---

Vielleicht sollte ich anmerken, das die Prüfung auf Gleichheit == technisch (maschinenzahl wandlung) immer problematisch ist. Wenn man auf einen Wert "nahe Null" prüft etwa

f(x) = If(floor(x) ≤ x < floor(x) + 1 / 2, x - floor(x), abs(x - floor(x) - 1 / 2) ≤ 10⁻^5, 0, floor(x) + 1 / 2 < x < floor(x) + 1, x - floor(x) - 1)

dann erhält man einen Sägezahn, was ggf. einem technischen Hintergrund besser entsprechen könnte?