Habe ich vielleicht die Polynomdivision irgendwo falsch angewendet?

Question

Aufgabe:

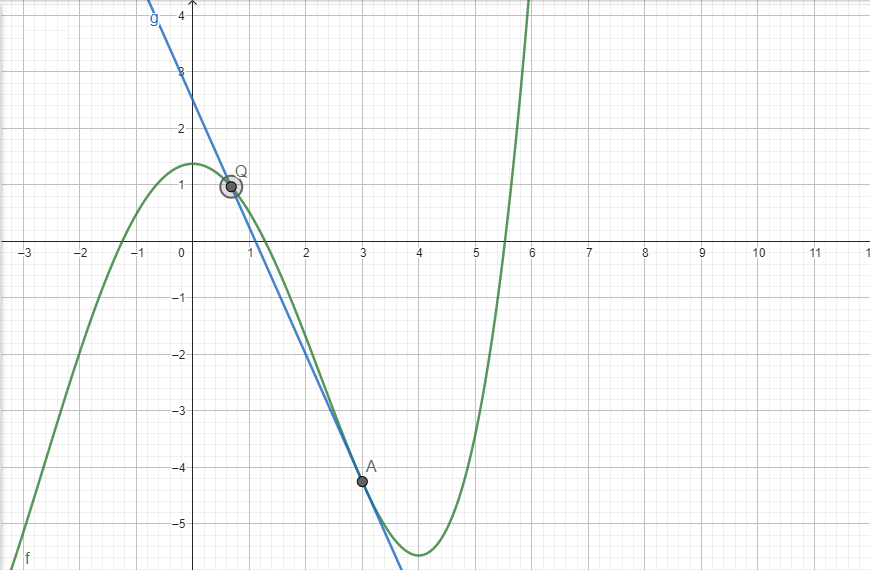
Ich muss einen Punkt Q bestimmen, der die Funktionen:

^{f(x) = $\frac{1}{40}$*x^4 + $\frac{1}{60}$*x³ - $\frac{9}{10}$*x² + $\frac{11}{8}$}

g(x)= -$\frac{9}{4}$*x^1 + $\frac{5}{2}$

schneidet.

Die Funktion g(x) ist dabei die Passante an dem Punkt A( 3 | -$\frac{17}{4}$ )

gesucht ist wie gesagt der Punkt Q.

Problem/Ansatz:

Da es sich um ein Schnittpunkt handelt, habe ich die beiden Funktionen gleichgesetzt und dann entsprechend umgestellt, sodass wir auf der einen Seite die umgestellte Funktion haben und auf der anderen Seite das Null (nach x ausrechnen um gleichen x-Wert beider Funktionen zu erhalten).

$\frac{1}{40}$*x^4 + $\frac{1}{60}$* x³ - $\frac{9}{10}$*x² + $\frac{9}{4}$*x^1 - $\frac{9}{8}$ = 0

Jetzt ist die Frage, wie ich die Nullstellen berechne. Die PQ Formel ist erst bei Funktionen 2-Grades möglich. Auch das Ausklammern der X-Variable wird nicht funktionieren, da noch eine Konstante in der Funktion ist, ohne eine Variable X.

Ich habe die Polynomfunktion durchgeführt und erstmal die Nullstellen geraten.

Für den ersten und zweiten Durchgang kann man für X=3 einsetzen, damit die Funktion 0 wird.

Das erste Zwischenergebnis war ohne Rest:

$\frac{1}{40}$*x³ + $\frac{11}{120}$*x² - $\frac{5}{8}$*x^1 + $\frac{3}{8}$


Noch immer ist das Ausklammern oder die PQ-Formel nicht möglich.

Das zweite Ergebnis hat leider bei mir einen Rest:

$\frac{1}{40}$*x² + $\frac{1}{12}$*x^1 - $\frac{3}{8}$ - $\frac{\frac{3}{4}}{x-3}$

- $\frac{\frac{3}{4}}{x-3}$ war der Rest, Wenn ich richtig liege.

Wie gehe ich weiter vor um die Nullstellen auszurechnen. Habe ich vielleicht die Polynomdivision irgendwo falsch angewendet?
Würde es auch eine andere Möglichkeit geben bei der ursprünglichen Funktionen f(x) und g(x), die Nullstellen zu berechnen?

Vielen Dank schon einmal

Comments

Schreibe doch bitte deine Aufgaben lesbarer auf; da schaut man gar nicht gut durch!
Benütze dazu die ganz linke Taste mit dem Zeichen  $\sqrt[4]{x}$. Danke.

---

Vielen Dank. Ich hatte gehofft, dass das Programm die Formatierung selbst vornimmt. Aber das war so mit den ganzen Klammer kaum lesbar. Das stimmt. Ich habe bereits den Anfang neu formatiert und bearbeite nun auch den Rest.

Answer 1

Hallo,

ich erweitere alle Koeffizienten erst einmal auf den Nenner 120.

3/120; 2/120; -108/120; 270/120; -135/120

Nun Polynomdivision durch (x-3) mit dem Horner-Schema:

	3	2	-108	270	-135
	/	9	33	-225	135
x=3	3	11	-75	45	0

Und noch einmal:

	3	11	-75	45
	/	9	60	-45
x=3	3	20	-15	0

Du musst also die Nullstellen von
(3x²+20x-15)/120
bestimmen.

Es gibt zwei Lösungen.

$x=\dfrac{-10\pm\sqrt{145}}{3}$

PS:

Deine zweite Polynomdivision war falsch.

Richtig wären die Koeffizienten 1/40; 1/6; -1/8

:-)

Comments

Ach perfekt! Das Horner-Schema ist auch wesentlich einfacher meiner Meinung nach.
Aufgrund deiner Erklärung habe ich es verstanden. Auch die Grafik war sehr hilfreich. Top!

Answer 2

Wodurch hast du dividiert, um das zu erhalten, was du 'Das zweite Ergebnis ' nennst? Eine kubische Gleichung, deren Lösung man nicht erraten kann, muss man entweder mit der Cardanischen Formel oder mit einem Näherungsverfahren lösen.

Comments

ich habe folgendes gerechnet, um auf das 'zweite Ergebnis' zu kommen:

( $\frac{1}{40}$*x₃ + $\frac{1}{120}$*x² - $\frac{5}{8}$*x^1 + $\frac{3}{8}$ ) / (x - 3) = $\frac{1}{40}$*x² + $\frac{1}{12}$*x^1 - $\frac{3}{8}$ - $\frac{\frac{3}{4}}{x-3}$

Die Verfahren kenne ich noch nicht. Dann muss ich sie mir erstmal aneignen. Danke!

Answer 3

Falls deine Annahmen und die Zeichnung wirklich stimmen, müsste man aus dem Term T(x) = f(x) - g(x)  den Faktor  (x-3) zweimal ausklammern können. Um das in einem einzigen Schritt zu erledigen, könntest du gleich die Division

       (f(x) - g(x)) / (x-3)²  =  (f(x) - g(x)) / (x² - 6x +9)

ausführen.

Falls nur die Funktionsterme gegeben waren (und du kein Plot-Programm hättest), wäre der Weg natürlich ein anderer:  Zuerst Lösungen bestimmen und erst dann zeichnen.

Comments

Vielen Dank. Ich muss das so mal ausprobieren

Answer 4

Alternativer Weg ohne Horner-Schema:

$f(x) = \frac{1}{40} *x^{4} + \frac{1}{60} *x^{3} - \frac{9}{10} *x^{2} + \frac{11}{8}$         $g(x)= - \frac{9}{4} *x + \frac{5}{2}$

$d(x)=f(x)-g(x)$

$d(x)= \frac{1}{40} *x^{4}+\frac{1}{60} *x^{3}-\frac{9}{10} *x^{2}+\frac{9}{4} *x-\frac{9}{8}$

Der Punkt $A( 3 | - \frac{17}{4})$ liegt auf der Geraden $g(x)$ und auf der Parabel 4. Grades:

$f(x)$  Somit liegt er auch auf $d(x)=f(x)-g(x)$.

$A( 3 | - \frac{17}{4})$

$d(3)= \frac{81}{40} +\frac{9}{20} -\frac{81}{10} +\frac{27}{4} -\frac{9}{8}=0$

$d´(3)= \frac{27}{10} +\frac{9}{20} -\frac{27}{5} +\frac{9}{4}=0$

Somit ist hier eine doppelte Nullstelle.

Polynomdivision:

$(\frac{1}{40} *x^{4}+\frac{1}{60} *x^{3}-\frac{9}{10} *x^{2}+\frac{9}{4} *x-\frac{9}{8}):(x-3)^2$ 

$(\frac{1}{40} *x^{4}+\frac{1}{60} *x^{3}-\frac{9}{10} *x^{2}+\frac{9}{4} *x-\frac{9}{8}):(x^2-6x+9)\\=\frac{1}{40}x^2 + \frac{1}{6}x - \frac{1}{8}$

$\frac{1}{40}x^2 + \frac{1}{6}x - \frac{1}{8}=0$

$x_1=\frac{1}{3}*\sqrt{145}-\frac{10}{3}$

$x_2=-\frac{1}{3}*\sqrt{145}-\frac{10}{3}$

Comments

Sehr cool! Ich wünschte ich könnte dir dafür noch einen Daumen hoch geben. Sehr detailliert wodurch ich die Polynomdivision noch besser verstehe und deren Anwendung. Vielleicht werde ich das selbst einmal jemand anderen beibringen. Auf jeden Fall sehr hilfreich. Vielen Dank Moliets!