Wie beweise ich eine K[T]-Modul Struktur mit einer neuen Skalarmultiplikation?

Question

Aufgabe:

Sei K ein Körper und V ein K-Vektorraum. Betrachte End(V) = {f : V → V lineare Abbildung}, und für f ∈ End(V), schreibe f_i : V → V für die i-fache Verknüpfung von f für i ≥ 1, und f_0 := idV

Zeigen Sie, dass jedes f ∈ End(V) eine K[T]-Modulstruktur auf V erzeugt, mit Skalarmultiplikation K[T] × V → V definiert als (T, v) 7→ T · v := f(v). (Das bedeutet, dass, wenn g = Σ(a_i * T^i) ∈ K[T], dann g · v := Σ(a_i * f_i(v)), für i ≥ 1 und f_0 := idV.)

Problem/Ansatz:

Nun muss ich ja alle R-Modul Axiome aufgreifen in der die skalar Multiplikation involviert ist und zeigen dass diese immer noch halten. Das wäre 1) Assoziativität bezgl. skalar mult. 2)Distributivität 3)1v=v

Nun scheitere ich aber schon bei 1):

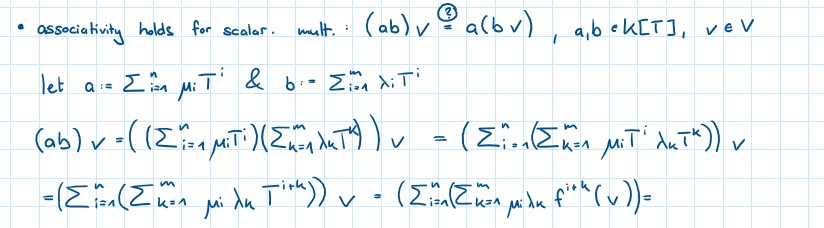
Text erkannt:

- associativity holds for scalar. mult.: \( (a b) \vee \stackrel{(3)}{=} a(b v), a, b \in K[T], v \in V \) let \( a:=\sum \limits_{i=1}^{n} \mu_{i} T^{i} \) \& \( b:=\sum \limits_{i=1}^{m} \lambda_{i} T^{i} \)
\( \begin{array}{l} (a b) v=\left(\left(\sum \limits_{i=1}^{n} \mu_{i} T_{i}\right)\left(\sum \limits_{k=1}^{m} \lambda_{k} T^{k}\right)\right) v=\left(\sum \limits_{i=1}^{n}\left(\sum \limits_{k=1}^{m} \mu_{i} T^{i} \lambda_{k} T^{k}\right)\right) v \\ =\left(\sum \limits_{i=1}^{n}\left(\sum \limits_{k=1}^{m} \mu_{i} \lambda_{k} T^{i+k}\right)\right) v=\left(\sum \limits_{i=1}^{n}\left(\sum \limits_{k=1}^{m} \mu_{i} \lambda_{k} f^{i+k}(v)\right)=\right. \end{array} \)

Komme nun nicht mehr weiter.. das Schlusslicht sollte ja a(bv) sein aber nach meinem Verständnis kann das nicht sein. Kann mir jemand weiter helfen? Vielen Dank

Answer 1

Ich glaube, du machst dir es hier zu schwer.

Wenn \(p(T) \in K[T]\), dann bedeutet die gegebene Definition

$$p(T)\cdot v = p(f)(v) \text{ für jedes } v \in V $$

Nun ist aber \(p(f) \in \operatorname{End}(V)\). Die Multiplikation in \(\operatorname{End}(V)\) ist die Verknüpfung der linearen Operatoren. Somit erhältst du für beliebige zwei Polynome \(p,q \in K[T]\) und beliebiges \(v \in V\):

$$p(T)\cdot (q(T) \cdot v ) = p(T)\cdot q(f)(v) = p(f)( q(f)(v))$$$$ = (p(f) \circ q(f))(v)=(p\cdot q)(f)(v) = (p\cdot q)(T)\cdot v$$

Hierbei wird die Tatsache benutzt, dass die Einsetzung

$$p(T) \mapsto p(f) \quad(K[T] \rightarrow \operatorname{End}(V))$$ein Ringhomomorphismus ist.