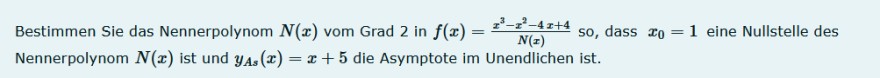
Bestimmen Sie das Nennerpolynom \( N(x) \) vom Grad 2 in \( f(x)=\frac{x^{3}-x^{2}-4 x+4}{N(x)} \) so, dass \( x_{0}=1 \) eine Nullstelle des Nennerpolynom \( N(x) \) ist und \( y_{A s}(x)=x+5 \) die Asymptote im Unendlichen ist.
Problem/Ansatz:
Ich habe leider keine Ahnung wie man N(x) bestimmt. Ich weiß zwar, dass die Nullstelle (x-1) eine Polstelle ist sowie, dass wenn ich den Zähler mit N(x) per Polynomdivision teile die Asymptote im Unendlichen x+5 heraus kommt, doch ich komme einfach nicht drauf.