Wo ist der Fehler bei meiner Lösung zu 2b?
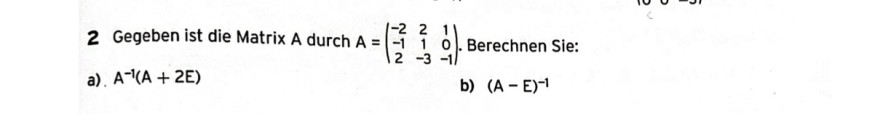
Text erkannt:
2 Gegeben ist die Matrix A durch \( A=\left(\begin{array}{ccc}-2 & 2 & 1 \\ -1 & 1 & 0 \\ 2 & -3 & -1\end{array}\right) \). Berechnen Sie:
a). \( A^{-1}(A+2 E) \)
b) \( (A-E)^{-1} \)

Text erkannt:
Nr.26.) \( (A-E)^{-1} \)
\( \begin{aligned} l-E & =\left(\begin{array}{ccc} -2 & 2 & 1 \\ -1 & 1 & 0 \\ 2 & -3 & -1 \end{array}\right)-\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) \\ & \sim\left(\begin{array}{ccc} -3 & 2 & 1 \\ -1 & 0 & 0 \\ 2 & -3 & -2 \end{array}\right)^{-1} \end{aligned} \)
\( \leadsto\left(\begin{array}{ccc} -3 & 2 & 1 \\ -1 & 0 & 0 \\ 2 & -3 & -2 \end{array}\right)^{-1} \)
\( \begin{array}{l} \left(\begin{array}{ccc|ccc} -3 & 2 & 1 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 & 1 & 0 \\ 2 & -3 & -2 & 0 & 0 & 1 \end{array}\right) \\ \left(\begin{array}{ccc|ccc} -3 & 2 & 1 & 1 & 0 & 0 \\ -2 & 0 & 0 & 0 & 2 & 0 \\ 2 & -3 & -2 & 0 & 0 & 1 \end{array}\right) 1+\text { III } \\ \left(\begin{array}{rrr|rrr} -3 & 2 & 1 & 1 & 0 & 0 \\ 0 & -3 & -2 & 0 & 2 & 1 \\ 2 & -3 & -2 & 0 & 0 & 1 \end{array}\right) \\ \left(\begin{array}{ccc|ccc} -3 & 2 & 1 & 1 & 0 & 0 \\ 0 & -3 & -2 & 0 & 2 & 1 \\ 3 & -\frac{8}{2} & -3 & 0 & 0 & \frac{3}{2} \end{array}\right) 1+I \\ \left(\begin{array}{ccc|ccc} -3 & 2 & 1 & 1 & 0 & 0 \\ 0 & -3 & -2 & 0 & 2 & 1 \\ 0 & -\frac{3}{2} & -2 & 1 & 0 & \frac{3}{2} \end{array}\right)_{1=\frac{5}{6}} \\ \left(\begin{array}{ccc|ccc} -3 & 2 & 1 & 1 & 0 & 0 \\ 0 & -3 & -2 & 0 & 2 & 1 \\ 0 & -3 & \frac{4}{5} & \frac{6}{5} & 0 & \frac{9}{5} \end{array}\right) 1-\text { III } \\ \left(\begin{array}{ccc|ccc} -3 & 2 & 1 & 1 & 0 & 0 \\ 0 & -3 & -2 & 0 & 2 & 1 \\ 0 & 0 & \frac{25}{5} & \frac{8}{5} & -2 & \frac{4}{5} \end{array}\right)^{1 \cdot 2} \\ \left(\begin{array}{ccc|ccc} -6 & 4 & 2 & 2 & 0 & 0 \\ 0 & -3 & -2 & 0 & 2 & 1 \\ 0 & 0 & \frac{27}{5} & \frac{6}{5} & -2 & \frac{4}{5} \end{array}\right)^{1+I I} \\ \end{array} \)
\( \begin{array}{l} \left(\begin{array}{ccc|ccc} -6 & 1 & 0 & 2 & 2 & 1 \\ 0 & -3 & -2 & 0 & 2 & 1 \\ 0 & 0 & \frac{22}{5} & \frac{6}{5} & -2 & \frac{1}{5} \end{array}\right) \\ \left(\begin{array}{ccc|ccc} 1 & \frac{1}{6} & 0 & -\frac{1}{3} & -\frac{1}{3} & -\frac{1}{6} \\ 0 & 1 & \frac{2}{3} & 0 & -\frac{2}{3} & -\frac{1}{3} \\ 0 & 0 & 1 & \frac{2}{11} & -\frac{5}{11} & \frac{2}{11} \end{array}\right) \\ \left(\begin{array}{ccc|ccc} 1 & \frac{1}{6} & 0 & -\frac{1}{3} & \frac{1}{3} & -\frac{1}{6} \\ 0 & 1 & \frac{2}{3} & 0 & -\frac{2}{3} & -\frac{1}{3} \\ 0 & 0 & -\frac{2}{3} & \frac{2}{11} & \frac{10}{33} & \frac{4}{33} \end{array}\right) 1+\text { III } \\ \left(\begin{array}{lll|lll} 1 & \frac{1}{3} & 0 & -\frac{1}{3} & -\frac{1}{3} & -\frac{1}{6} \\ 0 & 1 & 0 & -\frac{2}{11} & -\frac{4}{11} & -\frac{5}{11} \\ 0 & 0 & 1 & \frac{3}{11} & -\frac{5}{11} & \frac{2}{11} \end{array}\right) \end{array} \)