f(x) = - x^3 + 5·x^2 - 3·x + 10
f'(x) = - 3·x^2 + 10·x - 3
f''(x) = 10 - 6·x
Extrempunkte f'(x) = 0
- 3·x^2 + 10·x - 3 = 0
x = 1/3 ∨ x = 3
f(1/3) = 257/27 = 9.52 --> Tiefpunk
f(3) = 19 --> Hochpunkt
Wendepunkte f''(x) = 0
10 - 6·x = 0
x = 5/3
f(5/3) = 385/27 = 14.26
Skizze:
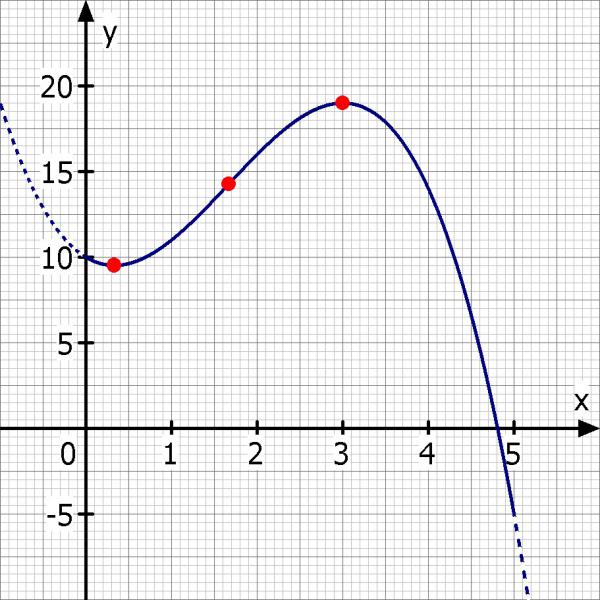
Du solltest mit meinen Rechnungen und der Skizze jetzt alle Fragen selbständig beantworten können.
Beachte: Meine Rechnungen beantworten noch nicht alleine die Fragestellungen.