Aufgabe:
Text erkannt:
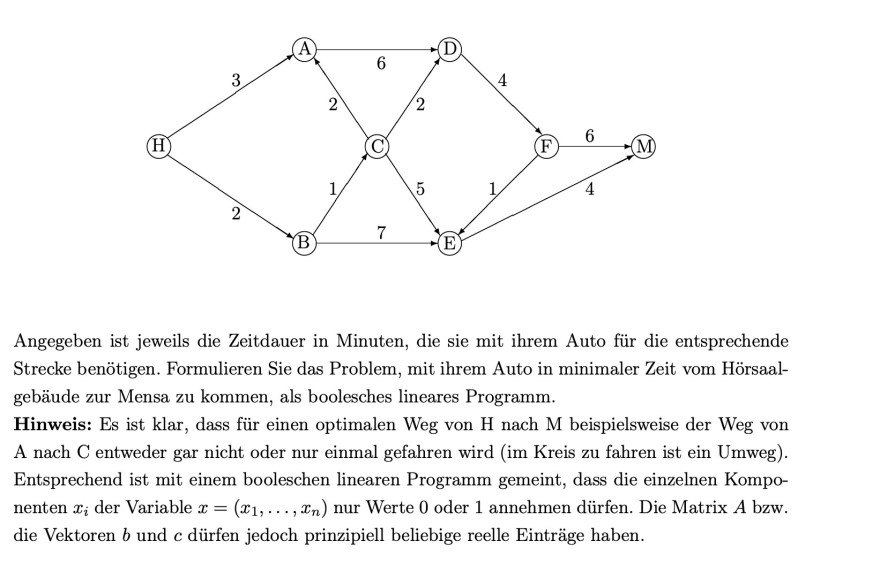
Angegeben ist jeweils die Zeitdauer in Minuten, die sie mit ihrem Auto für die entsprechende Strecke benötigen. Formulieren Sie das Problem, mit ihrem Auto in minimaler Zeit vom Hörsaalgebäude zur Mensa zu kommen, als boolesches lineares Programm.
Hinweis: Es ist klar, dass für einen optimalen Weg von \( \mathrm{H} \) nach \( \mathrm{M} \) beispielsweise der Weg von A nach \( \mathrm{C} \) entweder gar nicht oder nur einmal gefahren wird (im Kreis zu fahren ist ein Umweg). Entsprechend ist mit einem booleschen linearen Programm gemeint, dass die einzelnen Komponenten \( x_{i} \) der Variable \( x=\left(x_{1}, \ldots, x_{n}\right) \) nur Werte 0 oder 1 annehmen dürfen. Die Matrix \( A \) bzw. die Vektoren \( b \) und \( c \) dürfen jedoch prinzipiell beliebige reelle Einträge haben.
Problem/Ansatz:
Hallo, ich sitze schon seit längerem an dieser Aufgabe und habe Probleme das Szenario Mathematisch zu modellieren.
Ich habe mir Gedanken dazu gemacht und einen Ansatz formuliert.
Meine Frage ist also, wie man ein Lineares Programm zu diesem Szenario aufstellt?
Ich bedanke mich für jede Antwort!
Mein Ansatz:
es gibt n Wege von H nach M, die alle jeweils gesichtet sind mit w1, w2, w3..., wn. wi ist das Gewicht der Straße xi. Die Matrix besteht aus Einträgen xij, die entweder 0 oder 1 sind.
Zielfunktion:
minimiere Z = \( \sum\limits_{n=0}^{\infty}{wi * xi} \)
Der weg soll eine Verbindung zwischen Start (H) und Endpunkt (M) sein.
xi = 1, für die Straße, die von H aus genommen wird. Alle anderen Straßen xi = 0.
xj = 1 für die Straße, die zu M führt. Alle anderen xj = 0
Meine Nebenbedingungen lauten:
1.)xi = 1
2.) xj = 1
3.) jede Straße wird höchstens einmal genommen:
\( \sum\limits_{n=0}^{\infty}{xi} \) <= 1
4.) Die Einträge dürfen nicht negativ sein:
xij >= 0