Wie groß war die ursprüngliche Parkfläche?Wie groß ist die Fläche des neuen Parkplatzes?

Question

Aufgabe:

Viereck Berechnung, ich verstehe es einfach nicht

3. Ein Parkplatz soll vergrößert werden. Dazuwird die ursprüngliche Parkfläche (DreieckABC) zum Viereck ABCD erweitert.

Wie groß war die ursprüngliche Parkfläche?Wie groß ist die Fläche des neuen Parkplatzes?

Um wie viel Prozent vergrößert sich durchden Ausbau die Parkkapazität?

Siehe Foto ( hab es digital gemacht, aus der Tafelzeichnung)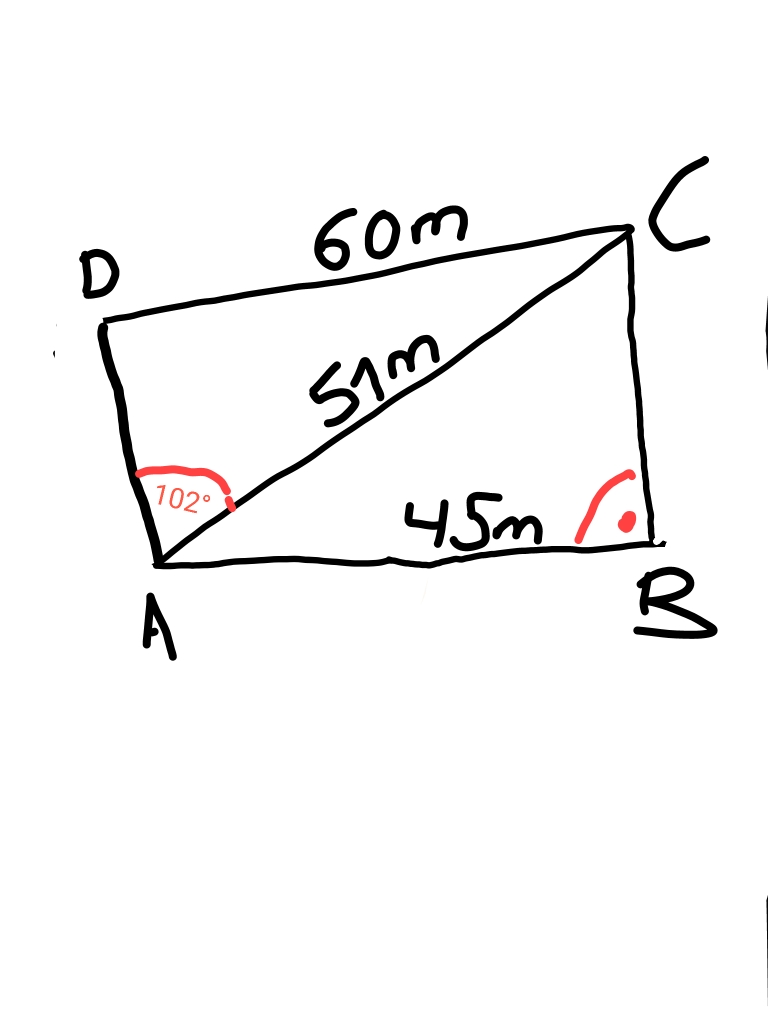

Problem/Ansatz:

Ich verstehe ehrlich gesagt nicht was ich machen soll, ich bräuchte eine Lösung mit Erklärung, damit ich die nächsten Aufgaben im Buch alleine lösen kann.

Ich war lange Krank und bin nicht fit in diesen Thema

Answer 1

Sinussatz und Flächenformel des Dreiecks sollten hier eigentlich gehen.

SIN(102°)/60 = SIN(δ)/51 --> δ = 56.25°

102 + 56.25 + γ = 180 --> γ1 = 21.75°

A1 = 1/2·60·51·SIN(21.75°) = 567.0 m²

Das nächste Dreieck ist sogar rechtwinklig, dann geht das noch einfacher.

COS(α°) = 45/51 --> α = 28.07°

A2 = 1/2·51·45·SIN(28.07°) = 540.0 m²

Answer 2

ABC ist ein rechtwinkliges Dreieck. AB² +BC² = AC². Daraus ergibt sich BC=24 m und die ursprüngliche Fläche ist 540 m². Wir machen weiter mit dem Sinussatz: 60m/sin(102°)=51m/sin(δ)

Aufgelöst nach δ ergibt δ≈56,25°. Damit ist γ≈21,75°. Jetzt kommt die Formel für Dreiecksflächen mit Sinus, also A=1/2·51 m·60 m·sin(γ)≈567,1 m². Das ist jetzt die zusätzliche Fläche ACD. Die neu Gesamtfläche ist somit ≈ 1107,1 m². Damit vergrößert sich die Parkfläche um 105%. Bitte melde dich, wenn die Zwischenschritte unklar sind.