Sets berechnen: Wie macht man?

Question

Aufgabe:

Text erkannt:

\( \begin{array}{c}M_{1}=\left\{x \in \mathbb{N}: x^{2}=16\right\}, \\ M_{2}=\left\{k \in \mathbb{N}: \sum \limits_{i=1}^{k} i \leq 16\right\} \\ M_{3}=\mathbb{N} \backslash\{x \in \mathbb{R}: x \geq 5\}\end{array} \)

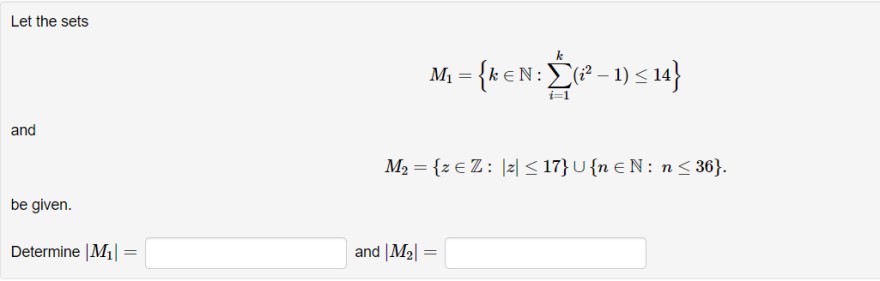
Text erkannt:

Let the sets
\( M_{1}=\left\{k \in \mathbb{N}: \sum \limits_{i=1}^{k}\left(i^{2}-1\right) \leq 14\right\} \)
and
\( M_{2}=\{z \in \mathbb{Z}:|z| \leq 17\} \cup\{n \in \mathbb{N}: n \leq 36\} . \)
be given.
Determine \( \left|M_{1}\right|= \) and \( \left|M_{2}\right|= \)

Aufgabe 2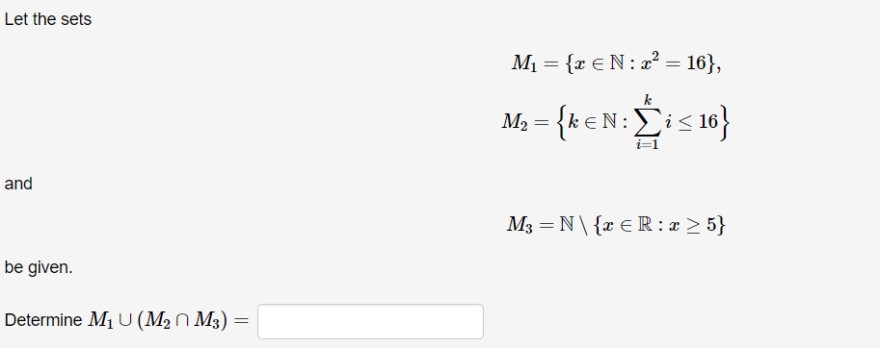

Text erkannt:

Let the sets
\( \begin{array}{c} M_{1}=\left\{x \in \mathbb{N}: x^{2}=16\right\}, \\ M_{2}=\left\{k \in \mathbb{N}: \sum \limits_{i=1}^{k} i \leq 16\right\} \end{array} \)
and
\( M_{3}=\mathbb{N} \backslash\{x \in \mathbb{R}: x \geq 5\} \)
be given.
Determine \( M_{1} \cup\left(M_{2} \cap M_{3}\right)= \)

Problem/Ansatz:

Aufageb1

Ich muss doch i bis zu einer zahl einsetzt die kleiner gleich 14 ist. Das ist 3. Das heißt das ist M1{3, 2, 1} und /M1/ = 3.

Ist bei M2 z also keine negative Zahl wegen den Betragsstrichen? also 0 bis 17? Und n 1 bis 36 und beides zusammen 0 bis 36? Ich verstehe das nicht ganz

Aufgabe 2

wäre ja x=4 M1={4} ?

Kann mir einer das erklären und die Lösung sagen?

Vielen Dank

Comments

Da sind 2 Aufgaben blättern jeweils M1,M2, (M3)

nenn die Mengen, von denen du grade sprichst nicht M1 usw, sondern schreib sie hin!

z∈ℤ und |z|<=17 sind alle ganzen Zahlen von -17 bis +17,  (denn etwa |-7|=7<17)dann vereinigt mit den  denn |natürlichen Zahlen <=36

zu 2, ja M1={4}

was ist noch unklar?

lul

Answer 1

2. Aufgabe:

\(  M_{1}=\left\{x \in \mathbb{N}: x^{2}=16\right\} =   \left\{ 4\right\} \)

\(  M_{2}=\left\{k \in \mathbb{N}: \sum \limits_{i=1}^{k} i \leq 16\right\} =   \left\{ 1,2,3,4,5\right\} \)

Wenn bei euch die nat. Zahlen mit 1 beginnen ist es

\( M_{3}=\mathbb{N} \backslash\{x \in \mathbb{R}: x \geq 5\} = \left\{ 1,2,3,4\right\} \)