ich habe ein Problem damit, anhand von Verteilungsfunktionen Wahrscheinlichkeiten auszurechen im diskreten Fall.
Ich glaube, mein Denkansatz ist dabei immer falsch, also vielleicht erläutere ich diesen mal anhand von ein paar Beispielen und ihr könntet mir sagen, wo ich da falsch herangehe?
Beispiel 1:
Ich habe folgende Wahrscheinlichkeitsfunktion:
f(1) = 0.2, f(2) = 0.1, f(3) = 0.2, f(4) = 0.5
Diese habe ich nun also Verteilungsfunktion geplottet:
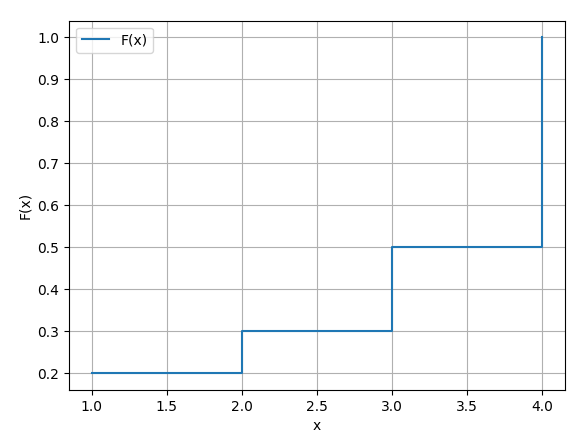
P(0 ≤ X ≤ 2): Die Zufallsvariable X liegt also zwischen einschließlich 0 und 2.
Anhand der Wahrscheinlichkeitsfunktion würde ich nun die Wahrscheinlichkeiten von 0 bis 2 aufaddieren.
Also: 0.2 + 0.1 = 0.3.
Mit der Verteilungsfunktion suche ich die "Fläche" (?) zwischen 0 und 2. Also X ≤ 2.. Die kann ich aus dem Graphen ablesen, weil das ja quasi nur die Definition der Verteilungsfunktion an der Stelle x = 2 ist. Also 0.3
P(2 ≤ X < 3): X zwischen einschließlich 2 und ohne 3.
F(3) - F(2) also: 0.3 - 0.2 = 0.1
Passt.
P(2 ≤ X ≤ 3): X ist also die Fläche zwischen 2 und 3.
Hier hätte ich jetzt das gleiche wie bei der vorherigen gerechnen, weil die Verteilungsfunktion ja sagt: X ist kleiner ODER gleich x.
Wohl aber falsch, da tatsächlich 0.3 herauskommt.
Kurz: Irgendwie habe ich hier einen Denkfehler drin. Und ohne Graphen wirds für mich noch schwieriger. Ich glaub einfach, dass ich das ganze irgendwie falsch angehe :(