Strahlensatz anwendbar auf Figur? Bekannt zwei Strecken und ein Schnittpunkt

Question

Man hat zwei bekannte Strecken:  Strecke AB= 30   Strecke EF=20 Schnittpunkt S0=10 gesucht  ist die Lila Strecke

 

Kann mir jmd. helfen komme hier nicht weiter ich weiß nicht ob der Strahlensatz überhaupt anwendbar ist

Danke !!!

 

Comments

Wie peinlich soll heißen Strahlensatz Anwendbar....

---

Ist 30 die Länge der grünen 'Diagonalen'?

Ist 20 die Länge der türkise 'Diagonalen' ?

10 senkrecht auf der lila Stecke?

Welche Winkel sind rechte Winkel? Der Schnittwinkel türkise - grün auch?

---

ja die Linien entsprechen der Länge und beginnen jeweils in den unteren Ecken und enden an den gegenüberliegenden (im rechten Winkel). Die Rote Linie ist der Schnittpunkt der beiden (dieser liegt bei 10) und ist Senkrecht auf der lila Linie gesucht ist die Länge der Lila Linie. (Zeichnung ist nicht Maßstabsgetreu) Hoffe jetzt ist mein problem präziser...

---

Wegen dem rechten Winkel in S0 sind ja die beiden Dreiecke mit der türkisen und der grünen Hypotenuse ähnlich.
Es gilt
30 : x = 20 : √(400 -x^2)

Daraus lässt sich x schon berechnen, ohne dass man die 10 braucht.

Vermutlich ist dieser Winkel nicht rechtwinklig. Vgl. Antwort von Unknown.

Answer 1

Ja, zusammen mit ein bisschen Pythagoras ist der Strahlensatz anwendbar.

Zunächst eine etwas ergänzte Skizze:

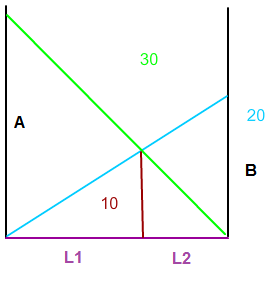
Ich habe die Lila Strecke L in zwei Teilstrecken L1 und L2 aufgeteilt (siehe Skizze), also L = L1 + L2.
Desweiteren bezeichne ich diejenige Strecke, die die beiden linken Randpunkte der grünen und der blauen Strecke verbindet, mit A und diejenige Strecke, die die beiden rechten Randpunkte der grünen und der blauen Strecke verbindet, mit B.

Mit Pythagoras gilt dann:

A = √ ( 30 ² - L ² )

sowie

B = √ ( 20 ² - L ² )

 

Nach Strahlensatz gilt:

L1 / 10 = L / B 

sowie

L2 / 10 = L / A

Aus L = L1 + L2 ergibt sich L1 = L - L2 . Setzt man zudem die Formeln für A und B ein, so erhält man:

( L - L2 ) / 10 = L / √ ( 20 ² - L ² )

sowie

L2 / 10 = L / √ ( 30 ² - L ² )

Das ist nun ein Gleichungssystem aus zwei Gleichungen mit zwei Unbekannten. Löst man dies (das ist eine schöne Übung, die ich gerne dir überlasse :-) ) , so findet man drei Lösungen für L:

L₁ ≈ - 12,312
L₂ = 0
L₃ ≈ 12,312

Nur die Lösung L₃ ist vorliegend sinnvoll.

Die lila Strecke L ist also etwa 12,312 Einheiten lang.

Comments

Erstmal Danke für die schnellen Antworten, ich scheitere aber schon an der mir gegebenen Übung  :-(  trotzdem würde ich gerne den Rechenweg verstehen wie man auf die Lösung kommt mich fuchst es so wenn ich etwas nicht verstehe.... eventuell kann sich nochmal jmd. erbarmen.

Vielen Dank und Gruß

---

Ich bekomme die Auflösung der Gleichungen nicht hin kann mir jmd. helfen.


Danke

Answer 2

Hi,

mal eine Lösungsmöglichkeit. Wird aber wahrscheinlich nicht die einfachste sein :/.

Aber sicher nachzuvollziehen.

 

Man erkennt zwei rechtwinklige Dreiecke (mit jeweils der grünen bzw. blauen Linie als Hypotenuse).

Es gilt also:

x^2+(p+q)^2 = 30^2

y^2+(p+q)^2 = 20^2

Da vier Unbekannte ist das nicht ausreichend. Nun noch Strahlensatz:

y/10 = (p+q)/p

x/10 = (p+q)/q

 

Das wöllte ich jetzt nicht von Hand lösen (habe ich auch nicht). Es ergeben sich 4 Lösungen, wobei nur eine Sinn ergibt, da nur hier alle Werte positiv sind:

p ≈ 7,8 und q ≈ 4,5 (sowie x ≈ 27,36 und y ≈ 15,76)

Lila Strecke ist damit: p+q ≈ 12,3 lang

Grüße